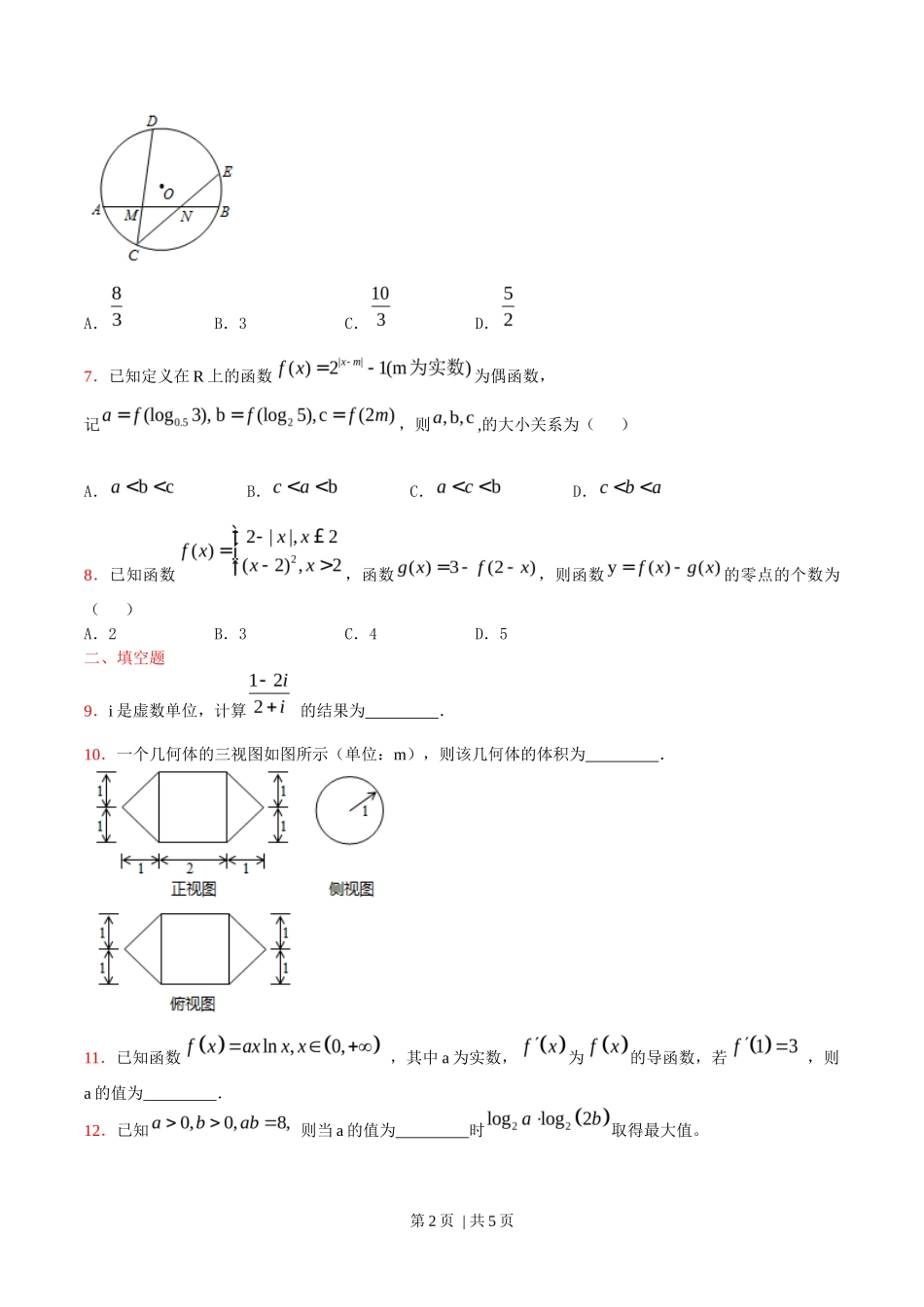
第 1 页 | 共 5 页 2015 年高考天津市文科数学真题一、选择题1.已知全集,集合,集合,则集合( )A.B.C.D.2.设变量满足约束条件,则目标函数的最大值为( )A.7B.8C.9D.143.阅读下边的程序框图,运行相应的程序,则输出 i 的值为( )A.2B.3C.4D.54.设,则“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件5.已知双曲线的一个焦点为,且双曲线的渐近线与圆相切,则双曲线的方程为( )A.B.C.D.6.如图,在圆 O 中,M,N 是弦 AB 的三等分点,弦 CD,CE 分别经过点 M,N,若 CM=2,MD=4,CN=3,则线段 NE 的长为( )第 2 页 | 共 5 页 A.B.3C.D.7.已知定义在 R 上的函数为偶函数,记,则,的大小关系为( )A.B.C.D.8.已知函数,函数,则函数的零点的个数为( )A.2B.3C.4D.5二、填空题9.i 是虚数单位,计算 的结果为 .10.一个几何体的三视图如图所示(单位:m),则该几何体的体积为 .11.已知函数 ,其中 a 为实数,为的导函数,若 ,则a 的值为 .12.已知 则当 a 的值为 时取得最大值。第 3 页 | 共 5 页 13.在等腰梯形 ABCD 中,已知, 点 E 和点 F 分别在线段 BC 和CD 上,且 则的值为 .14.已知函数 若函数在区间内单调递增,且函数的图像关于直线对称,则的值为 .三、解答题15.设甲、乙、丙三个乒乓球协会的运动员人数分别为 27,9,18,先采用分层抽样的方法从这三个协会中抽取 6 名运动员参加比赛。(Ⅰ)求应从这三个协会中分别抽取的运动员人数;(Ⅱ)将抽取的 6 名运动员进行编号,编号分别为,从这 6 名运动员中随机抽取 2 名参加双打比赛。(i)用所给编号列出所有可能的结果;(ii)设 A 为事件“编号为的两名运动员至少有一人被抽到”,求事件 A 发生的概率。16 . △ ABC 中 , 内 角 A,B,C 所 对 的 边 分 别 为 a , b , c , 已 知 △ ABC 的 面 积 为, (Ⅰ)求 a 和 sinC 的值;(Ⅱ)求 的值。17.如图,已知平面 ABC, AB=AC=3,,, 点 E,F 分别是 BC, 的中点,(Ⅰ)求证:EF 平面 ;(Ⅱ)求证:平面平面。(Ⅲ)求直线 与平面所成角的大小。第 4 页 | 共 5 页 18.已知是各项均为正数的等比数列,是等差数列,且,.(Ⅰ)求和的通项公式;(Ⅱ)设,求数列的前 n 项和.19.已知椭圆的上顶点为 B,左焦点为,离心率为.(Ⅰ)求直线 BF 的斜率;(Ⅱ)设直线 BF 与椭圆交于点 P(P 异于点 B),故点 B 且垂直于 BF 的直线与椭圆交于点 Q(Q 异于点B)直线 PQ 与 x 轴交于点 M,.(i)求的值;(ii)若,求椭圆的方程.20.已知函数其中,且.(Ⅰ)求的单调区间;(Ⅱ)设曲线与轴正半轴的交点为 P,曲线在点 P 处的切线方程为,求证:对于任意的实数,都有;第 5 页 | 共 5 页 (Ⅲ)若方程有两个正实数根且,求证:.