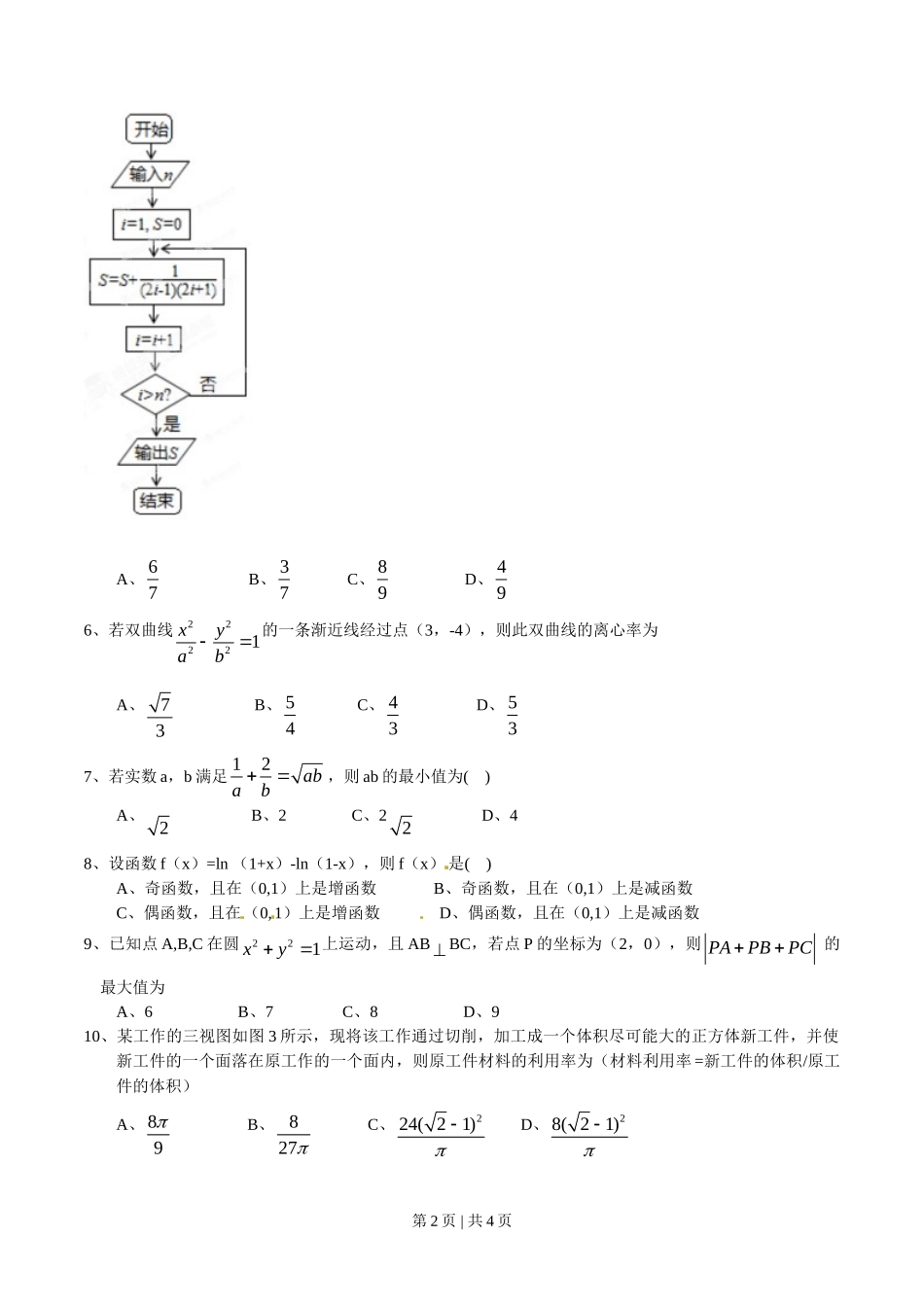
一、选择题:本大题共 10 小题,每小题 5 分,共 50 分,在每小题给出的四个选项中,只有一项是符合题目要求的.1、 已知2(1)iz=1+i(i 为虚数单位),则复数 z=( )A、1+i B、1-i C、-1+i D、-1-i 2、 在一次马拉松比赛中,35 名运动员的成绩(单位:分钟)如图 I 所示;若将运动员按成绩由好到差编为 1~35 号,再用系统抽样方法从中抽取 7 人,则其中成绩在区间[139,151]上的运动员人数为( )A、3 B、4 C、5 D、63、设 xR,则“x>1”是“2x>1”的( ) A、充分不必要条件 B、必要不充分条件C、充要条件 D、既不充分也不必要条件4、若变量 x、y 满足约束条件111xyyxx ,则 z=2x-y 的最小值为( )A、-1 B、0 C、1 D、25、执行如图 2 所示的程序框图,如果输入 n=3,中输入的 S=( )第 1 页 | 共 4 页 A、 67 B、 37 C、 89 D、 496、若双曲线22221xyab 的一条渐近线经过点(3,-4),则此双曲线的离心率为A、73 B、 54 C、 43 D、 537、若实数 a,b 满足 12abab,则 ab 的最小值为( )A、2 B、2 C、22 D、48、设函数 f(x)=ln (1+x)-ln(1-x),则 f(x) 是( )A、奇函数,且在(0,1)上是增函数 B、奇函数,且在(0,1)上是减函数C、偶函数,且在(0,1)上是增函数 D、偶函数,且在(0,1)上是减函数9、已知点 A,B,C 在圆221xy 上运动,且 AB BC,若点 P 的坐标为(2,0),则 PAPBPC� 的最大值为A、6 B、7 C、8 D、910、某工作的三视图如图 3 所示,现将该工作通过切削,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工作的一个面内,则原工件材料的利用率为(材料利用率 =新工件的体积/原工件的体积)A、 89 B、 827 C、224( 21) D、28( 21) 第 2 页 | 共 4 页 二、填空题:本大题共 5 小题,每小题 5 分,共 25 分.11、已知集合 U=1,2,3,4 ,A=1,3 ,B=1,3,4 ,则 A(U Bð)=_____.12、在直角坐标系 xOy 中,以坐标原点为极点 ,x 轴正半轴为极轴建立极坐标系.若曲线 C 的极坐标方程为2sin,则曲线 C 的直角坐标方程为_____.[来源:学科网 ZXXK]13. 若直线 3x-4y+5=0 与圆2220xyrr相交于 A,B 两点,且120oAOB(O 为坐标原点),则r=_____ .14、若函数 f(x)=| 2x -2 |-b 有两个零点,则实数 b 的取值范围是_____.15、已知 >0,在函数 y=2sin x 与 y=2cos x 的图像的交点中,距离最短的两个交点的距离为 2 3 ,则 =_____.三、解答题:本大题共 6 小题,共 75 分,解答应写出文字说明,证明过程或演算步骤。16. 本小题满分 12 分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有 2 个红球12,A A 和 1 个白球 B 的甲箱与装有 2 个红球12,a a 和 2 个白球12,b b 的乙箱中,各随机摸出 1 个球,若摸出的 2 个球都是红球则中奖,否则不中奖。[来源:Zxxk.Com](I)用球的标号列出所有可能的摸出结果;(II)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。17. 本小题满分 12 分)设 ABC的内角, ,A B C 的对边分别为 , , ,tana b c abA。(I)证明:sincosBA;(II) 若3sinsincos4CAB,且 B 为锐角,求, ,A B C 。18. 本小题满分 12 分)如图 4,直三棱柱111ABCA B C的底面是边长为 2 的正三角形,,E F 分别是第 3 页 | 共 4 页 1,BC CC 的中点。(I)证明:平面 AEF 平面11B BCC ;(II)若直线1AC 与平面11A ABB 所成的角为45 ,求三棱锥 FAEC的体积。[来源:学。科。网 Z。X。X。K]19. 本小题满分 13 分)设数列{}na的前n 项和为nS ,已知121,2aa ,且13nnaS *13,()nSnN,[来源:学科网 ZXXK](I)证明:23nnaa ;(II)求nS 。20. 本小题满分 13 分)已知抛物线21 :4Cxy的焦点 F 也是椭圆22222:1yxCab[来源:学.科.网](0)ab的一个焦点,1C 与2C 的公共弦长为 2 6 ,过点 F 的直线l 与1C 相交于,A B 两点,与2C相交于,C D 两点,且 AC�与 BD�同向。(I)求2C 的方程;(II)若 ACBD,求直线l 的斜率。21. 本小题满分 13 分)函数2( )cos ([0,)f xaex x ,记nx 为( )f x 的从小到大的第*()n nN个极值点。(I)证明:数列{ ()}nf x是等比数列;(II)若对一切*,()nnnNxf x恒成立,求a 的取值范围。 第 4 页 | 共 4 页