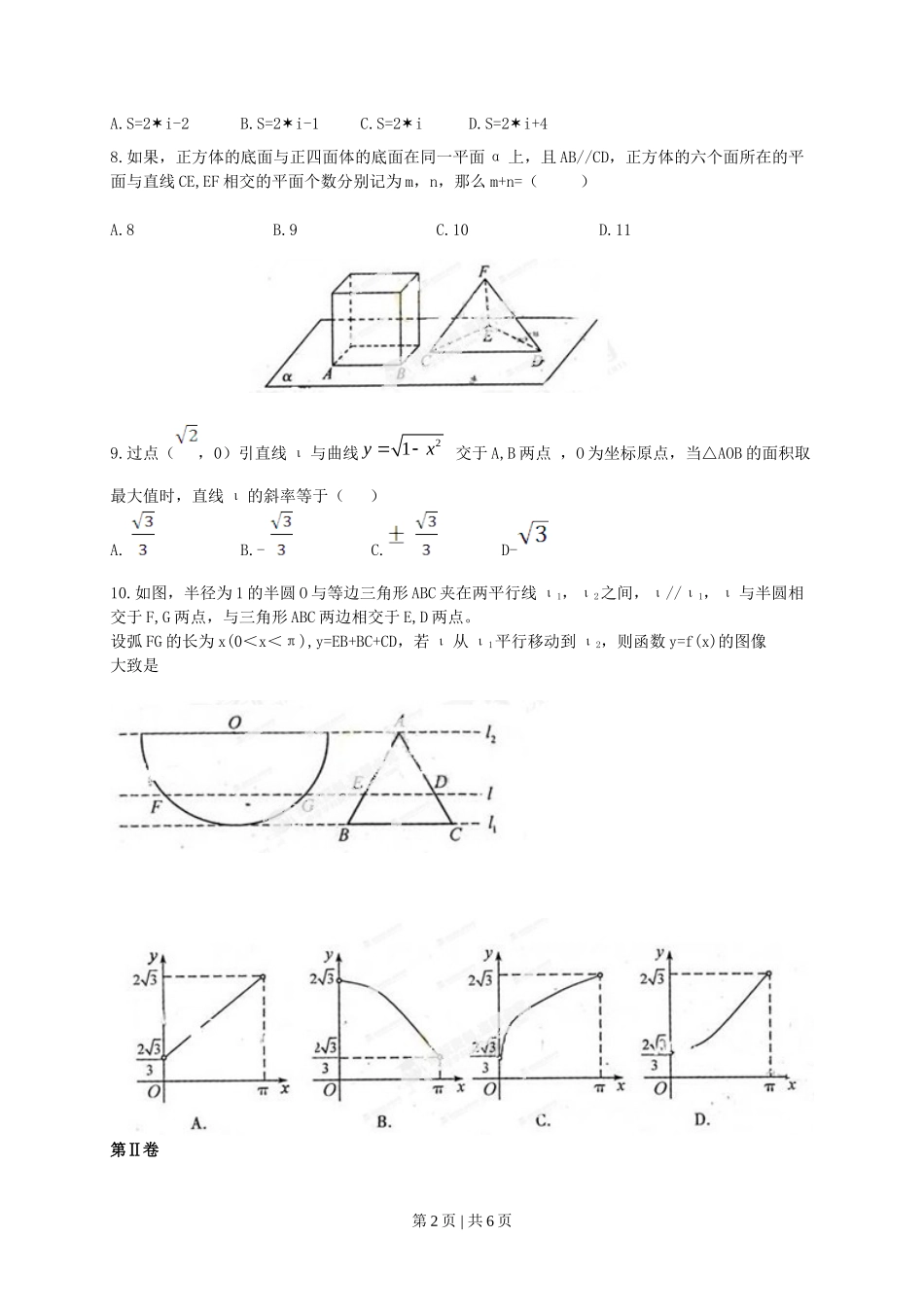
第Ⅰ卷(选择题 共 50 分)一、选择题:本大题共 10 小题。每小题 5 分,共 50 分。在每个小题给出的四个选项中,只有一项是符合题目要求的。1.设集合 M={1,2,zi},i 为虚数单位,N={3,4},M∩N={4},则复数 z= ()A. -2i B. 2iC. -4iD.4i2.函数的定义域为()A.(0,1)B.[0,1)C.(0,1]D.[0,1]3.等比数列 x,3x+3,6x+6,…的的第四项等于()A.-24B.0C.12D.244.总体由编号为 01,02,…,19,20 的 20 个个体组成.利用下面的随机数表选取 5 个个体,选取方法从随机数表第 1 行的第 5 列和第 6 列数字开始由左到右一次选取两个数字,则选出来的第 5 个个体的编号为()7816 6572 0802 6314 0702 4369 9728 01983204 9234 4934 8200 3623 4869 6938 7481A.08B.07C.02D.015.2531()xx展开式中的常数项为()A.80B.-80C.40D.-406.22221231111,,,xSx dx Sdx Se dxx若 ,则 s1,s2,s3的大小关系为( )A. s1<s2<s3B. s2<s1<s3C. s2<s3<s1D. s3<s2<s17.阅读如下程序框图,如果输出 i=5,那么在空白矩形框中应填入的语句为第 1 页 | 共 6 页 A.S=2 i-2B.S=2 i-1 C.S=2 iD.S=2 i+48.如果,正方体的底面与正四面体的底面在同一平面 α 上,且 AB//CD,正方体的六个面所在的平面与直线 CE,EF 相交的平面个数分别记为 m,n,那么 m+n=( )A.8B.9C.10D.119.过点(,0)引直线 ι 与曲线21yx 交于 A,B 两点 ,O 为坐标原点,当△AOB 的面积取最大值时,直线 ι 的斜率等于( )A.B.-C.D-10.如图,半径为 1 的半圆 O 与等边三角形 ABC 夹在两平行线 ι1,ι2之间,ι//ι1,ι 与半圆相交于 F,G 两点,与三角形 ABC 两边相交于 E,D 两点。设弧 FG 的长为 x(0<x<π),y=EB+BC+CD,若 ι 从 ι1平行移动到 ι2,则函数 y=f(x)的图像大致是第Ⅱ卷第 2 页 | 共 6 页 注意事项:第卷共 2 页,须用黑色墨水签字笔在答题卡上书写作答。若在试题卷上作答,答案无效。二.填空题:本大题共 4 小题,每小题 5 分,共 20 分 11.函数 y=sin2x+2sin2x 的最小正周期 T 为_______. 12.设 e1,e2为单位向量。且 e1、e2的夹角为 ,若 a=e1+3e2,b=2e1,则向量 a 在 b 方向上的射影为________. 13.设函数 f(x)在(0,+∞)内可导,且 f(ex)=x+ex,则(1)f =__________. 14.抛物线 x2=2py(p>0)的焦点为 F,其准线与双曲线 - =1 相交于 A,B 两点,若△ABF为等边三角形,则 p=___________.三.选做题:请在下列两题中任选一题作答,若两题都做按其中一题评阅计分。本题共 5 分。15(1)(坐标系与参数方程选做题)设曲线 C 的参数方程为:x=t,y=t2 (t 为参数),若以直角坐标系的原点为极点,x 轴的正半轴为极轴简历极坐标系,则曲线 C 的极坐标方程为_______.(2)(不等式选做题)在实数范围内,不等式211x 的解集为___________.四.解答题:本大题共 6 小题,共 75 分。解答应写出文字说明、证明过程或演算步骤。16.(本小题满分 12 分)在△ABC 中,角 A,B,C 所对的边分别为 a,b,c,已知cos(cos3sin)cos0.CAAB(1)求角 B 的大小;(2)若 a+c=1,求 b 的取值范围.17.(本小题满分 12 分)正项数列{an}的前 n 项和 Sn满足:222(1)()0nnSnnSnn(1)求数列{an}的通项公式 an;(2)令221(2)nnnbna,数列{bn}的前 n 项和为 Tn.证明:对于任意 n N*,都有 Tn< 5 .6418.(本小题满分 12 分)小波以游戏方式决定是参加学校合唱团还是参加学校排球队,游戏规则为:以 0 为起点,再从1A ,2345678,,,,,,A A A A A A A (如图)这 8 个点中任取两点分别分终点得到两个向量,记这两个向量的数量积为 X。若 X=0 就参加学校合唱团,否则就参加学校排球队。第 3 页 | 共 6 页 (1)求小波参加学校合唱团的概率;(2)求 X 的分布列和数学期望。19(本小题满分 12 分)如图,四棱锥 P-ABCD ...