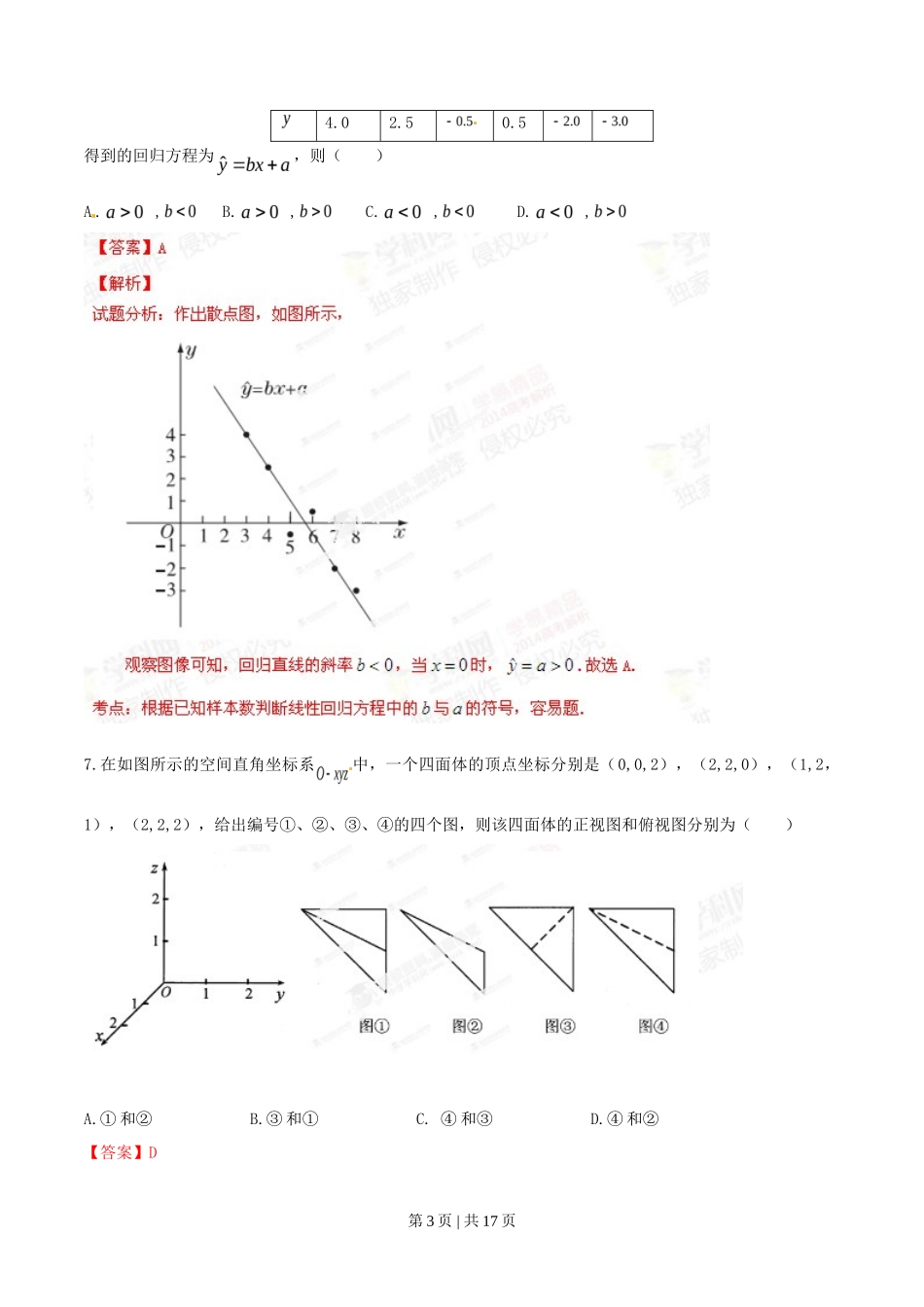
一.选择题:本大题共 10 小题,每小题 5 分,共 50 分. 在每小题给出的四个选项中,只有一项是符合题目要求的。1. 已知全集,集合,则( )A. B. C. D. 2. 为虚数单位,则( )A. B. C. D.3. 命题“,”的否定是( )[来源:学&科&网 Z&X&X&K]A. , B. , C. , D. ,4.若变量 、满足约束条件,则的最大值是( )第 1 页 | 共 17 页 A.2 B.4 C.7 D.85.随机投掷两枚均匀的投骰子,他们向上的点数之和不超过 5 的概率为,点数之和大于 5 的概率为,点数之和为偶数的概率为,则( )A. B. C. D. 6.根据如下样本数据:3[来源:学+科+网]45678第 2 页 | 共 17 页 4.02.50.5得到的回归方程为,则( )A . , B. , C. , D. ,7.在如图所示的空间直角坐标系中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )A.① 和② B.③ 和① C. ④ 和③ D.④ 和② 【答案】D 第 3 页 | 共 17 页 8.设 、 是关于 的方程的两个不等实根,则过,两点的直线与双曲线的公共点的个数为( )A. 0 B. 1 C. 2 D. 3 第 4 页 | 共 17 页 9.已知是定义在上的奇函数,当时,,则函数的零点的集合为( )A. B. C. D.10.《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“盖”的术:置 如其周,令相承也.又以高乘之,三十六成一.该术相当于给出了有圆锥的底面周长与高,计算其体积的近似公式它实际上是将圆锥体积公式中的圆周率近似取为 3. 那么近似公式相当于将圆锥体积公式中的近似取为( )A. B. C. D.[来源:学科网 ZXXK]第 5 页 | 共 17 页 二.填空题:本大题共 7 小题,每小题 5 分,共 35 分.请将答案填在答题卡对应题号的位置上,答错位置,书写不清,模棱两可均不得分.11.甲、乙两套设备生产的同类产品共 4800 件,采用分层抽样的方法从中抽取一个容量为 80 的样本进行检测.若样本中有 50 件产品由甲设备生产,则乙设备生产的产品总数为__ ______件.12.若向量,,,则________.13.在中,角、、所对的边分别为 、 、 ,已知,,,则________.第 6 页 | 共 17 页 14.阅读如图所示的程序框图,运行相应的程序,若输入 的值为 9,则输出的值为 .15.如图所示,函数的图象由两条射线和三条线段组成.若,,则正实数的取值范围是 .第 7 页 | 共 17 页 16.某项研究表明,在考虑行车安全的情况下,某路段车流量(单位时间内测量点的车辆数,单位:辆/小时)与车流速度 ( 假设车辆以相同速度 行驶,单位:米/秒)平均车长 (单位:米)的值有关,其公式为(1)如果不限定车型,,则最大车流量为_______辆/小时;(2)如果限定车型,,则最大车流量比(1)中的最大车流量增加 辆/小时.17. 已知圆和点,若定点和常数 满足:对圆上那个任意一点第 8 页 | 共 17 页 ,都有,则:(1) ;(2) .所以,解得或(舍去).故.考点:圆的性质,两点间的距离公式,二元二次方程组的解法,难度中等.三、解答题:本大题共 5 小题,共 65 分.解答应写出文字说明、证明过程或演算步骤.18.(本小题满分 12 分)某实验室一天的温度(单位:)随时间 (单位: )的变化近似满足函数关系;.(1)求实验室这一天上午 8 时的温度;(2)求实验室这一天的最大温差. 第 9 页 | 共 17 页 故实 验室这一天最高温度为 12 ,最低温度为 8 ,最大温差为 4 . 考点:三角函数的实际运用,两个角的和的正弦公式,三角函数的最值.19.(本小题满分 12 分)已知等差数列满足:,且、、成等比数列.(1)求数列的通项公式.(2)记为数列的前 项和,是否存在正整数 ,使得若存在,求 的最小值;若不存在,说明理由.第 10 页 | 共 17 页 20.(本小题满分 13 分)[来源:学*科*网 Z*X*X*K]如图,在正方体中,,,,,,分别是棱,,, ,,的中点. 求证:第 11 页 ...