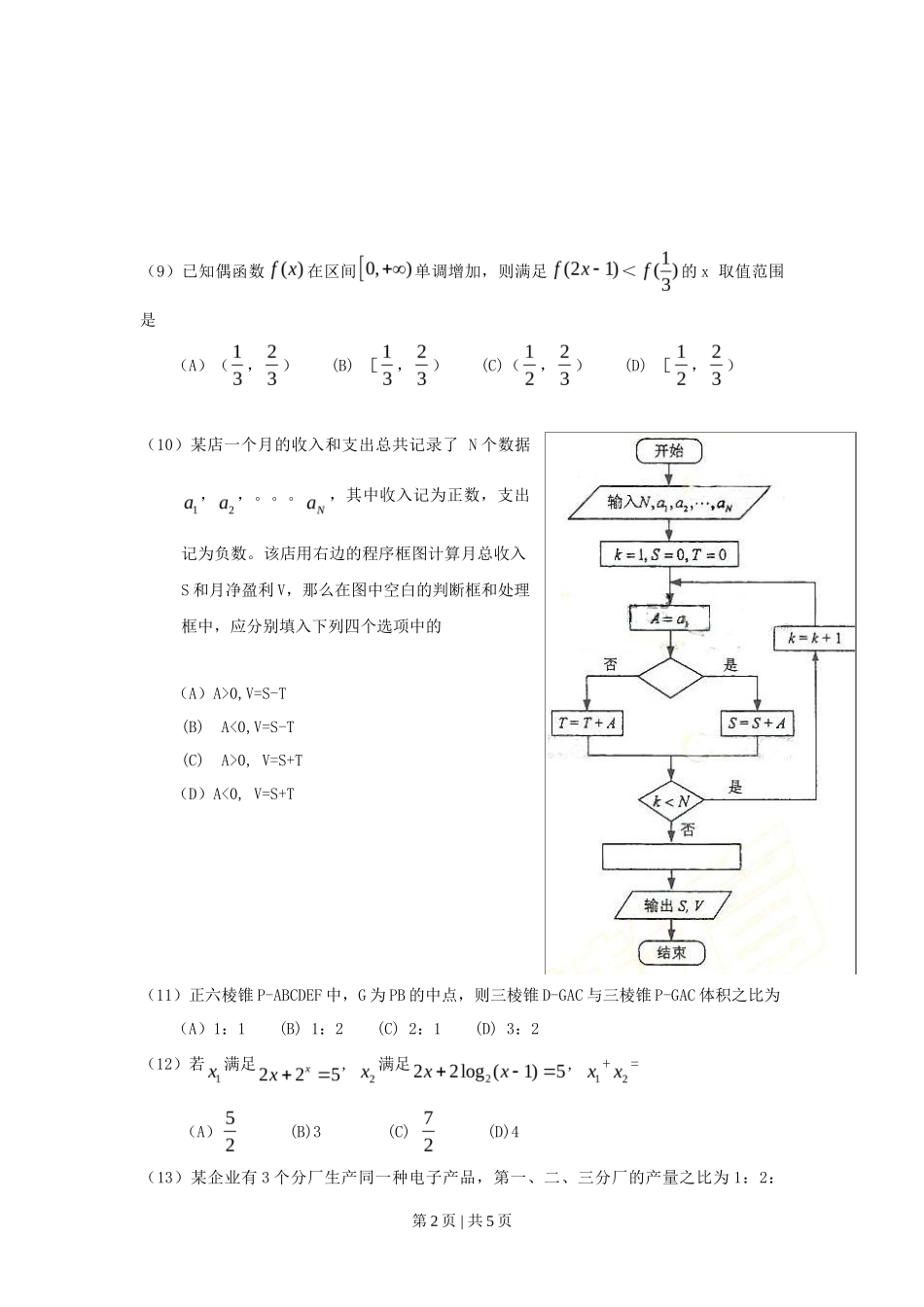
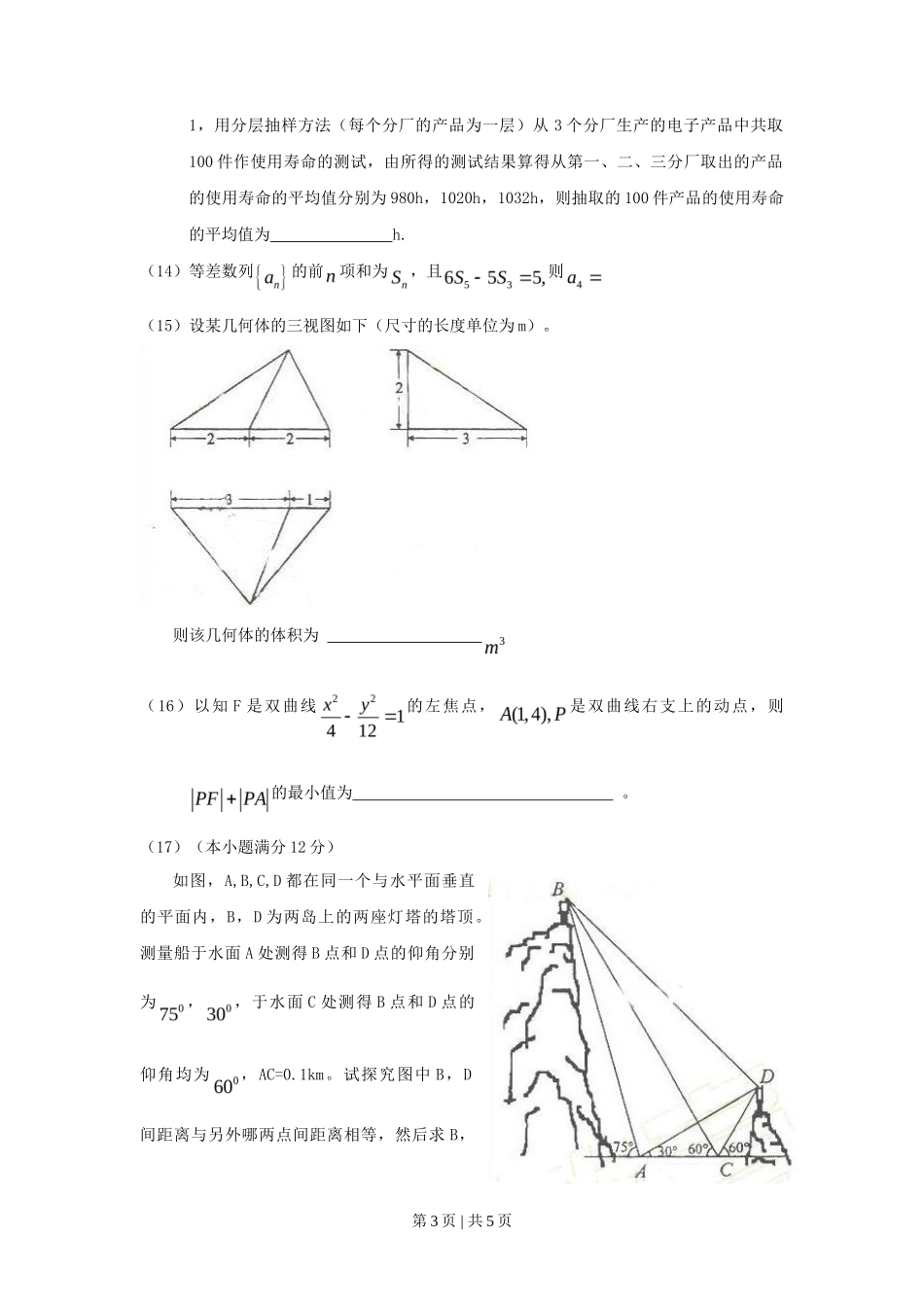
2009 年辽宁高考理科数学真题一- 选择题(每小题 5 分,共 60 分)(1)已知集合 M={x|-30,V=S-T (B) A<0,V=S-T (C) A>0, V=S+T(D)A<0, V=S+T(11)正六棱锥 P-ABCDEF 中,G 为 PB 的中点,则三棱锥 D-GAC 与三棱锥 P-GAC 体积之比为(A)1:1 (B) 1:2 (C) 2:1 (D) 3:2(12)若满足, 满足, +=(A) (B)3 (C) (D)4(13)某企业有 3 个分厂生产同一种电子产品,第一、二、三分厂的产量之比为 1:2:第 2 页 | 共 5 页 1,用分层抽样方法(每个分厂的产品为一层)从 3 个分厂生产的电子产品中共取100 件作使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分别为 980h,1020h,1032h,则抽取的 100 件产品的使用寿命的平均值为 h.(14)等差数列的前项和为,且则 (15)设某几何体的三视图如下(尺寸的长度单位为 m)。则该几何体的体积为 (16)以知 F 是双曲线的左焦点,是双曲线右支上的动点,则的最小值为 。(17)(本小题满分 12 分)如图,A,B,C,D 都在同一个与水平面垂直的平面内,B,D 为两岛上的两座灯塔的塔顶。测量船于水面 A 处测得 B 点和 D 点的仰角分别为,,于水面 C 处测得 B 点和 D 点的仰角均为,AC=0.1km。试探究图中 B,D间距离与另外哪两点间距离相等,然后求 B,第 3 页 | 共 5 页 D 的距离(计算结果精确到 0.01km,1.414,2.449)(18)(本小题满分 12 分)如图,已知两个正方行 ABCD 和 DCEF 不在同一平面内,M,N 分别为 AB,DF 的中点。(Ⅰ)若平面 ABCD ⊥平面 DCEF,求直线 MN 与平面 DCEF 所成角的正值弦;(Ⅱ)用反证法证明:直线 ME 与 BN 是两条异面直线。(19)(本小题满分 12 分)某人向一目射击 4 次,每次击中目标的概率为。该目标分为 3 个不同的部分,第一、二、三部分面积之比为 1:3:6。击中目标时,击中任何一部分的概率与其面积成正比。(Ⅰ)设 X 表示目标被击中的次数,求 X 的分布列;(Ⅱ)若目标被击中 2 次,A 表示事件“第一部分至少被击中 1 次或第二部分被击中 2次”,求 P(A)(20)(本小题满分 12 分)已知,椭圆 C 过点 A,两个焦点为(-1,0),(1,0)。(Ⅰ)求椭圆 C 的方程;(Ⅱ)E,F 是椭圆 C 上的两个动点,如果直线 AE 的斜率与 AF 的斜率互为相反数,证明直线 EF 的斜率为定值,并求出这个定值。(21)(本小题满分 12 分)已知函数(Ⅰ)讨论函数的单调性;(Ⅱ)证明:若,则对任意 x ,x,xx ,有。第 4 页 | 共 5 页 请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。做答时用 2B 铅笔在答题卡上把所选题目的题号涂...