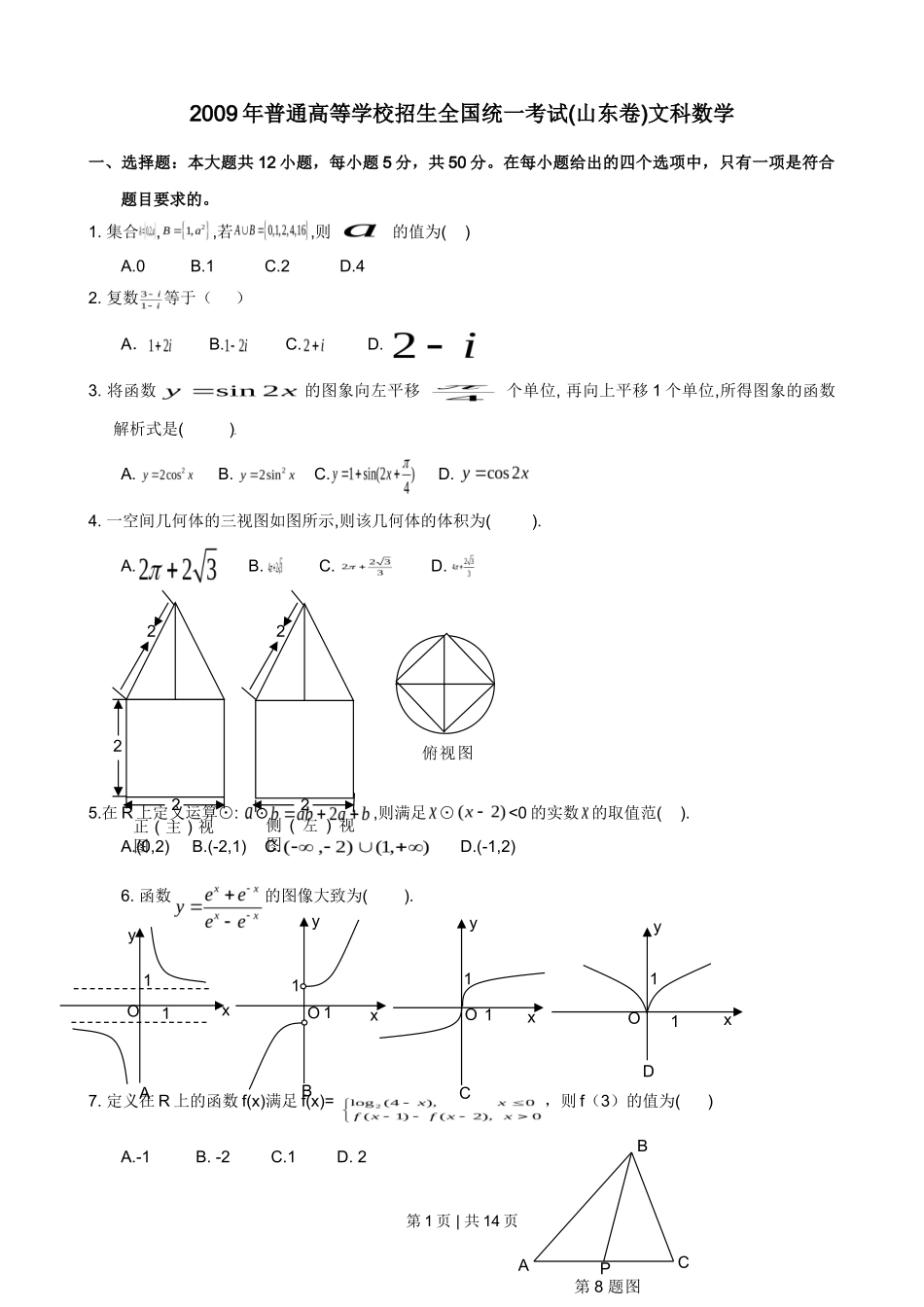
2009 年普通高等学校招生全国统一考试(山东卷)文科数学一、选择题:本大题共 12 小题,每小题 5 分,共 50 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1. 集合,,若,则的值为( )A.0 B.1 C.2 D.42. 复数等于( )A. B. C. D.3. 将函数的图象向左平移个单位, 再向上平移 1 个单位,所得图象的函数解析式是( )A. B. C. D. 4. 一空间几何体的三视图如图所示,则该几何体的体积为( ).A. B. C. D. 5.在 R 上定义运算⊙: ⊙,则满足 ⊙<0 的实数 的取值范( ).A.(0,2) B.(-2,1) C. D.(-1,2)6. 函数的图像大致为( ).7. 定义在 R 上的函数 f(x)满足 f(x)= ,则 f(3)的值为( )A.-1 B. -2 C.1 D. 2第 1 页 | 共 14 页 2 2 侧 ( 左 ) 视图 2 2 2 正 ( 主 ) 视图 1 x y 1 O A x y O 1 1 B x y O 1 1 C x y 1 1 D O A B C P 第 8 题图 俯视图 8.设 P 是△ABC 所在平面内的一点,,则( )A. B. C. D.9. 已知 α,β 表示两个不同的平面,m 为平面 α 内的一条直线,则“”是“”的( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件10. 设斜率为 2 的直线 过抛物线的焦点 F,且和轴交于点 A,若△OAF(O 为坐标原点)的面积为 4,则抛物线方程为( )A. B. C. D. 11.在区间上随机取一个数 x,的值介于 0 到之间的概率为( ).A. B. C. D.12. 已知定义在 R 上的奇函数,满足,且在区间[0,2]上是增函数,则( ).A. B. C. D. 第Ⅱ卷二、填空题:本大题共 4 小题,每小题 4 分,共 16 分。13.在等差数列中,,则.14.若函数 f(x)=a -x-a(a>0 且 a 1)有两个零点,则实数 a 的取值范围是 . 15.执行右边的程序框图,输出的 T= .16.某公司租赁甲、乙两种设备生产 A,B 两类产品,甲种设备每天能生产 A 类产品 5 件和 B 类产品 10 件,乙第 2 页 | 共 14 页 开始 S=0,T=0,n=0 T>S S=S+5 n=n+2 T=T+n 输出 T 结束 是 否 种设备每天能生产 A 类产品 6 件和 B 类产品 20 件.已知设备甲每天的租赁费为 200 元,设备乙每天的租赁费为 300 元,现该公司至少要生产 A 类产品 50 件,B 类产品 140 件,所需租赁费最少为__________元.三、解答题:本大题共 6 小题,共 74 分。17.(本小题满分 12 分)设函数 f(x)=2在处取最小值.(1)求 的值;(2)在ABC 中,分别是角 A,B,C 的对边,已知,求角 C.18.(本小题满分 12 分) 如图,在直四棱柱 ABCD-A B C D 中,底面 ABCD 为等腰梯形,AB//CD,AB=4, BC=CD=2, AA=2, E、E 分别是棱 AD、AA 的中点(Ⅰ)设 F 是棱 AB 的中点,证明:直线 EE //平面 FCC ;(Ⅱ)证明:平面 D1AC⊥平面 BB1C1C.19. (本小题满分 12 分) 一汽车厂生产 A,B,C 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):轿车 A轿车 B轿车 C舒适型100150z标准型300450600按类型分层抽样的方法在这个月生产的轿车中抽取 50 辆,其中有 A 类轿车 10 辆.(1)求 z 的值(2)用分层抽样的方法在 C 类轿车中抽取一个容量为 5 的样本.将该样本看成一个总体,从中任取 2 辆,求至少有 1 辆舒适型轿车的概率;(3)用随机抽样的方法从 B 类舒适型轿车中抽取 8 辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这 8 辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过 0.5 的概率.20.(本小题满分 12 分)等比数列{}的前 n 项和为,已知对任意的,点,均在函数且均为常数)的图像上(1)求 r 的值;第 3 页 | 共 14 页 E A B C F E1 A1 B1 C1 D1 D (11)当 b=2 时,记 求数列的前 项和21.(本小题满分 12 分)已知函数,其中(1)当满足什么条件时,取得极值?(2)已知,且在区间上单调递增,试用 表示出 的取值范围.22. (本小题满分 14 分)设,在平面直角坐标系中,已知向量,向量,,动...