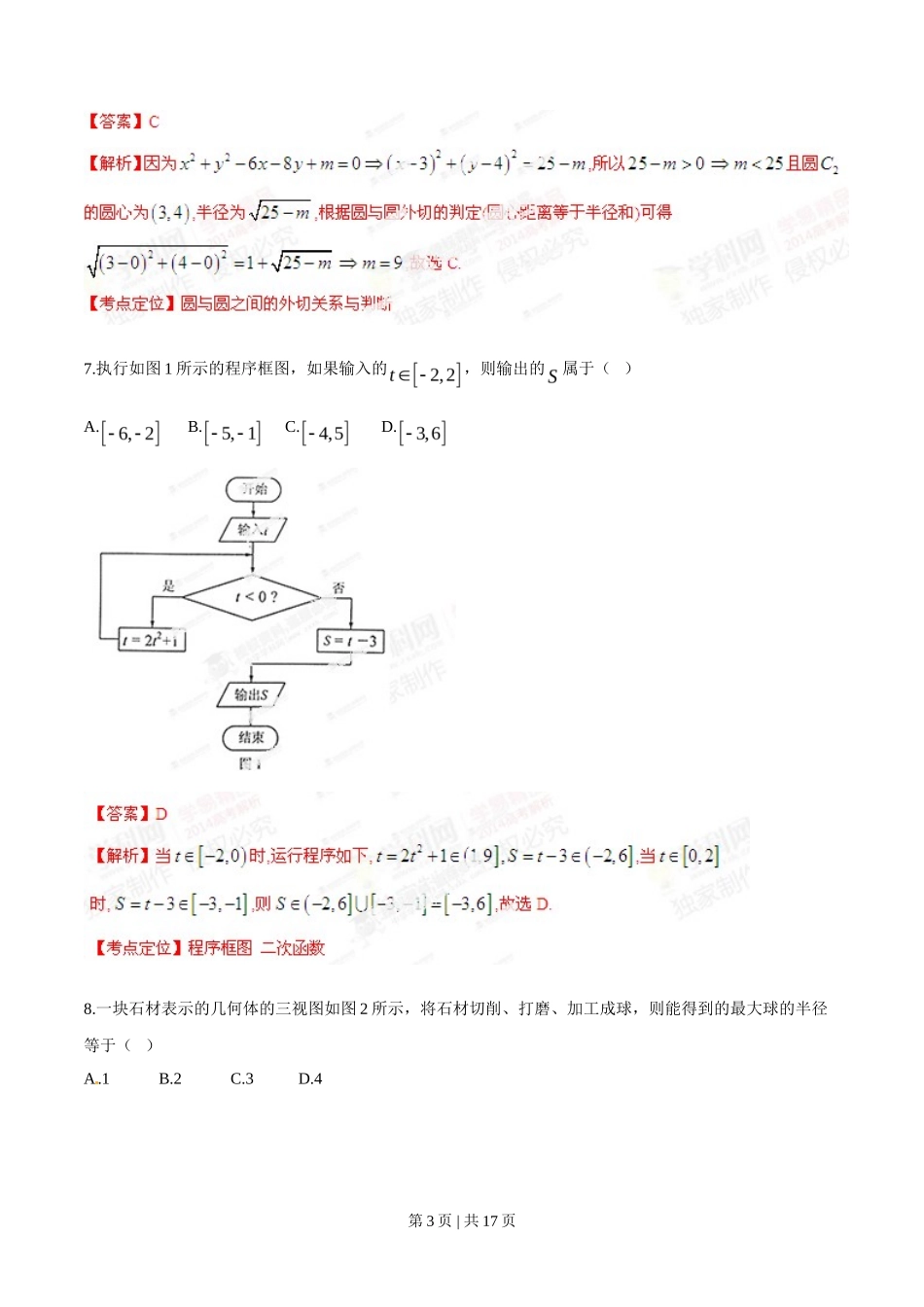
一.选择题:本大题共 10 小题,每小题 5 分,共 50 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设命题,则为( ) 2.已知集合,则( ) 【答案】C[来源:学&科&网]【解析】由交集的定义可得,故选 C.【考点定位】集合交集3.对一个容量为的总体抽取容量为的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为,则( ) 第 1 页 | 共 17 页 4.下列函数中,既是偶函数又在区间上单调递增的是( ) 5.在区间上随机选取一个数,则的概率为( ) 6.若圆与圆,则( ) 第 2 页 | 共 17 页 7.执行如图 1 所示的程序框图,如果输入的,则输出的属于( )A. B. C. D.8.一块石材表示的几何体的三视图如图 2 所示,将石材切削、打磨、加工成球,则能得到的最大球的半径等于( )A.1 B.2 C.3 D.4第 3 页 | 共 17 页 9.若,则( )A.B.C. D.1 0.在平面直角坐标系中,为原点,,,,动点满足,[来源:学_科_网 Z_X_X_K]则的取值范围是( )第 4 页 | 共 17 页 A. B.C. D.[来源:学|科|网 Z|X|X|K]二.填空题:本大题共 5 小题,每小题 5 分,共 25 分.11.复数( 为虚数单位)的实部等于_________.12.在平面直角坐标系中,曲线( 为参数)的普通方程为___________.[来源:学科网]第 5 页 | 共 17 页 13.若变量满足约束条件,则的最大值为_________.14.平面上以机器人在行进中始终保持与点的距离和到直线的距离相等.若机器人接触不到过点且斜率为 的直线,则 的取值范围是___________.第 6 页 | 共 17 页 15.若是偶函数,则____________.三、解答题:本大题共 6 小题,共 75 分.解答应写出文字说明,证明过程或演算过程.16.(本小题满分 12 分)已知数列的前 项和.(1)求数列的通项公式;(2)设,求数列的前项和.【答案】(1) (2) 【解析】试题分析:(1)题目已知之间的关系,令,利用,即可求的的值,令,利用与前 n 项和之间的关系即可得到,令检验首项即可得到的通项公式.第 7 页 | 共 17 页 17.(本小题满分 12 分)某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年研发新产品的结果如下:其中分别表示甲组研发成功和失败;分别表示乙组研发成功和失败.(1)若某组成功研发一种新产品,则给改组记 1 分,否记 0 分,试计算甲、乙两组研发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;(2)若该企业安排甲、乙两组各自研发一种新产品,试估算恰有一组研发成功的概率.【答案】(1) ,,, ,甲组优于乙组 (2) 第 8 页 | 共 17 页 18.(本小题满分 12 分)如图 3,已知二面角的大小为,菱形在面内,两点在棱上,,是的中点,面,垂足为.(1)证明:平面;(2)求异面直线与所成角的余弦值.第 9 页 | 共 17 页 [来源:学科网]第 10 页 | 共 17 页 19.(本小题满分 13 分)如图 4,在平面四边形中,,(1)求的值;(2)求的长第 11 页 | 共 17 页 (2)由题设可得,于是根据正余弦之间的关系可得,而,所以,在中,,第 12 页 | 共 17 页 所以.【考点定位】正余弦定理 正余弦和差角公式 直角三角形 正余弦之间的关系20. (本小题满分 13 分)如图 5,为坐标原点,双曲线和椭圆均过点,且以的两个顶点和的两个焦点为顶点的四边形是面积为 2 的正方形.(1)求的方程;(2)是否存在直线 ,使得 与交于两点,与只有一个公共点,且?证明你的结论.第 13 页 | 共 17 页 的值,利用之间的关系即可求出的值,得到椭圆的标准方程.第 14 页 | 共 17 页 第 15 页 | 共 17 页 21.(本小题满分 13 分)已知函数.(1)求的单调区间;(2)记为的从小到大的第个零点,证明:对一切,有.. 第 16 页 | 共 17 页 【考点定位】导数 单调性 放缩法 裂项求和 第 17 页 | 共 17 页