2014年高考数学试卷（理）（重庆）（解析卷）

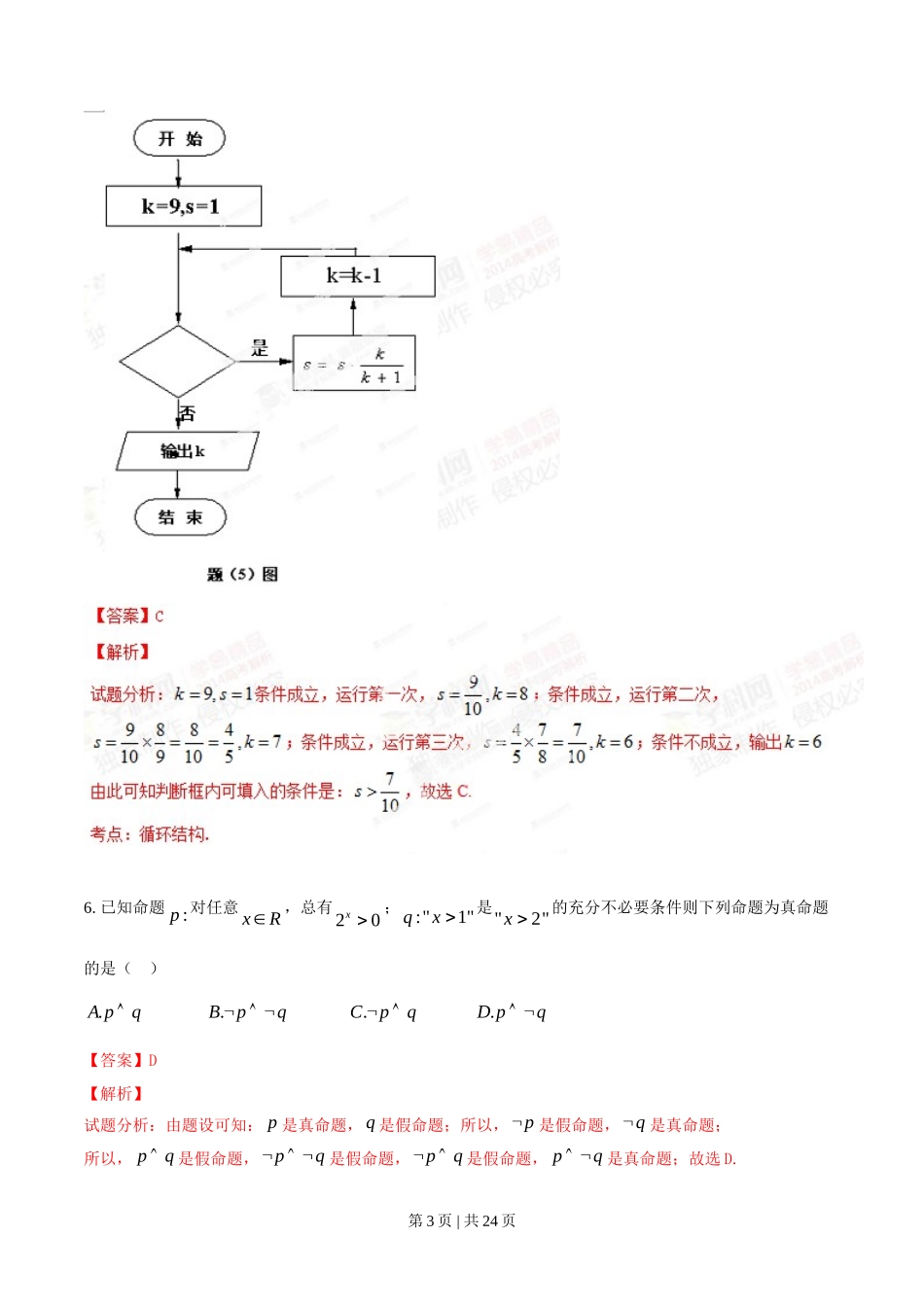
一.选择题：本大题共 10 小题，每小题 5 分，共 50 分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.复平面内表示复数 (12 )ii的点位于( ).A 第一象限 .B 第二象限.C 第三象限 .D 第四象限2. 对任意等比数列{}na,下列说法一定正确的是( )139. ,,A a a a 成等比数列 236.,,B a a a 成等比数列248.,,C a a a 成等比数列 369.,,D a a a 成等比数列3. 已知变量 x 与 y 正相关，且由观测数据算得样本平均数3x  ，3.5y ，则由该观测的数据算得的线性回归方程可能是( )第 1 页 | 共 24 页 .0.42.3A yx .22.4B yx.29.5C yx .0.34.4C yx4. 已知向量( ,3),(1,4),(2,1)akbc，且(23 )abc，则实数k =（ ）9.2A  .0B .C 3 D.1525.执行如题（5）图所示的程序框图，若输出k 的值为 6，则判断框内可填入的条件是（ ）A.12s  B.35s  C.710s  D.45s 第 2 页 | 共 24 页 6. 已知命题:p 对任意 xR，总有20x ；:"1"qx 是"2"x 的充分不必要条件则下列命题为真命题的是（ ）.A pq .Bpq   .Cpq  .D pq 【答案】D【解析】试题分析：由题设可知： p 是真命题，q 是假命题；所以，p是假命题，q是真命题；所以， pq是假命题，pq  是假命题，pq 是假命题， pq 是真命题；故选 D.第 3 页 | 共 24 页 考点：1、指数函数的性质；2、充要条件；3、判断复合命题的真假.学科 zxxk7.某几何体的三视图如图所示，则该几何体的表面积为（ ）A.54 B.60 C.66 D.72【答案】B【解析】试题分析：第 4 页 | 共 24 页 8.设21FF，分别为双曲线)0,0(12222babyax的左、右焦点，双曲线上存在一点 P 使得,49||||,3||||2121abPFPFbPFPF则该双曲线的离心率为（ ）A. 34 B. 35 C. 49 D.39.某次联欢会要安排 3 个歌舞类节目、2 个小品类节目和 1 个相声类节目的演出顺序，则同类节目不相邻的排法种数是( )第 5 页 | 共 24 页 A.72 B.120 C.144 D.16810.已知 ABC的内角21)sin()sin(2sin,BACCBAACBA满足，，面积 S 满足 CBAcbaS,,,,21分别为，记所对的边，则下列不等式一定成立的是( )A.8)(cbbc B.()16 2ac ab C.126abc D.1224abc【答案】A二、填空题.11. 设全集{|110},{1,2,3,5,8},{1,3,5,7,9},()UUnNnABAB 则 ð______.第 6 页 | 共 24 页 所以答案应填：14.考点：1、对数的运算；2、二次函数的最值.13. 已知直线02  yax与圆心为C 的圆4122ayx相交于BA， 两点，且 ABC为等边三角形，则实数a_________.考生注意：14、15、16 三题为选做题，请从中任选两题作答，若三题全做，则按前两题给分.14. 过圆外一点 P 作圆的切线 PA （ A 为切点），再作割线 PBC 分别交圆于 B 、C ， 若6PA，第 7 页 | 共 24 页 AC=8，BC=9，则 AB=________.【答案】4【解析】试题分析：由切割线定理得：2PAPBPC,设 PBx ，则|| 9PCx 所以，369 ,x x即29360xx ，解得：12x （舍去），或3x 又由是圆的切线，所以ACPBAP,所以 ACPBAP、||||||PAABACPC,所以8 6412AB所以答案应填：4.考点：1、切割线定理；2、三角形相似.15. 已知直线l 的参数方程为tytx32（t 为参数），以坐标原点为极点， x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2sin4cos00,02 ，则直线l 与曲线C 的公共点的极径________.第 8 页 | 共 24 页 16.若不等式2212122aaxx对任意实数 x 恒成立，则实数a 的取值范围是____________.第 9 页 | 共 24 页 由图可知： min1522f xf ,由题意得：215222aa，解这得:11,2a 所以答案应...