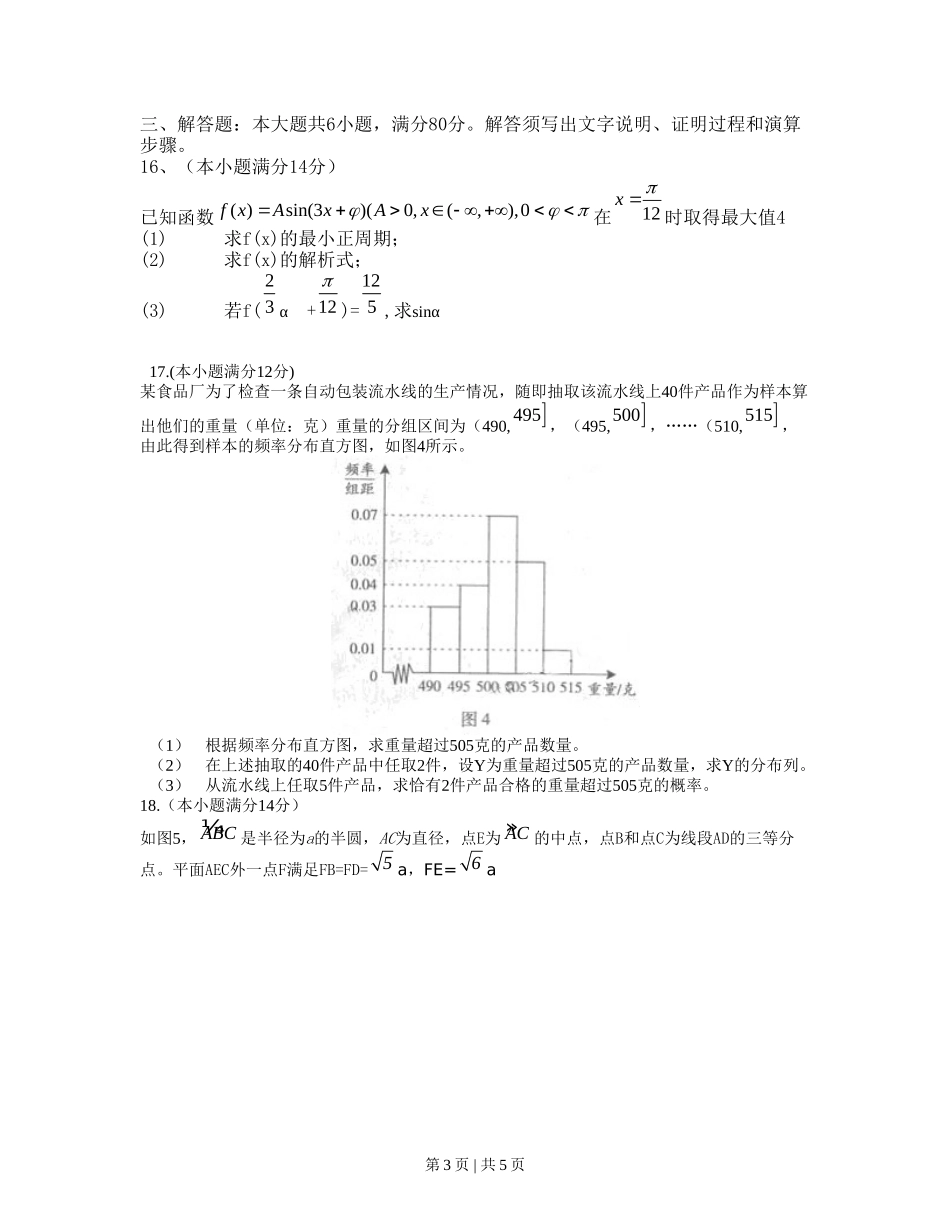
绝密 ★ 启用前2010年普通高等学校招生全国统一考试(广东A卷)数学(理科)一、选择题:本大题共8小题,每小题5分,满分40分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.若集合A={-2< x <1},B={ x 0< x <2}则集合A ∩ B=A. { x -1< x <1} B. { x -2< x <1}C. { x -2< x <2} D. { x 0< x <1}2.若复数z1=1+i,z2=3-i,则z1·z2=A.4 B. 2+ i C. 2+2 i D.33.若函数f(x)=3x+3-x与g(x)=3x-3-x的定义域均为R,则A.f(x)与g(x)均为偶函数 B. f(x)为偶函数,g(x)为奇函数A.f(x)与g(x)均为奇函数 B. f(x)为奇函数,g(x)为偶函数4. 4.已知{}na为等比数列,Sn是它的前n项和。若2312aaa, 且4a 与27a 的等差中项为54 ,则5S =A.35 B.33 C.31 D.295. “14m ”是“一元二次方程20xxm ”有实数解“的A.充分非必要条件 B.充分必要条件C.必要非充分条件 D.非充分必要条件6.如图1,△ ABC为三角形, AA// BB //CC , CC ⊥平面ABC 且3 AA=32 BB=CC =AB,则多面体△ABC - A B C 的正视图(也称主视图)是ABCD w_w w.k*s_5 u.c o_m7已知随机变量X服从正态分布N(3.1),且p(2 ≤X ≤4)=0.6826,则p(X>4)=A、0.1588 B、0.1587 C、0.1586 D0.15858.为了迎接2010年广州亚运会,某大楼安装5个彩灯,它们闪亮的顺序不固定,每个彩灯彩灯第 1 页 | 共 5 页 闪亮只能是红、橙、黄、绿、蓝中的一种颜色,且这5个彩灯商量的颜色各不相同。记这这5个彩灯有序地闪亮一次为一个闪烁,在每个闪烁中,每秒钟有且仅有一个彩灯闪亮,而相邻两个闪烁的时间间隔均为5妙。如果要实现所有不同的闪烁,那么需要的时间至少是A、 1205秒 B.1200秒 C.1195秒 D.1190秒二、填空题:本大题共7小题,考生作答6小题,每小题5分,满分30分。(一)必做题(9-13题)w_w w.k*s_5 u.c o_m9. 函数( )f x =lg( x -2)的定义域是 .10.若向量ar=(1,1,x), br=(1,2,1), cr=(1,1,1),满足条件() (2 )cabrrr=-2,则 x = .11.已知a,b,c分别是△ABC的三个内角A,B,C所对的边,若a=1,b= 3 , A+C=2B,则sinC= .12.已知圆心在x轴上,半径为2 的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是 w_w w.k*s_5 u.c o_m13.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1…xn(单位:吨),根据图2所示的程序框图,若n=2,且x1,x2 分别为1,2,则输出地结果s为 . w_w w.k*s_5 u.c o_m14、(几何证明选讲选做题)如图3,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD=23a,∠OAP=30°,则CP=______. w_w w.k*s_5 u.c o_m 15、(坐标系与参数方程选做题)在极坐标系(ρ,θ)(0 ≤ θ<2π)中,曲线ρ=2sin 与cos1p 的交点的极坐标为______。 第 2 页 | 共 5 页 三、解答题:本大题共6小题,满分80分。解答须写出文字说明、证明过程和演算步骤。16、(本小题满分14分)已知函数( )sin(3)(0,(,),0f xAxAx 在12x时取得最大值4 (1) 求f(x)的最小正周期;(2) 求f(x)的解析式;(3) 若f(23 α +12)=125 ,求sinα w_w w.k*s_5 u.c o_m17.(本小题满分12分)某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为(490,495 ,(495,500 ,……(510,515 ,由此得到样本的频率分布直方图,如图4所示。(1)根据频率分布直方图,求重量超过505克的产品数量。(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列。(3)从流水线上任取5件产品,求恰有2件产品合格的重量超过505克的概率。18.(本小题满分14分)w_w w.k*s_5 u.c o_m如图5, ¼ABC 是半径为a的半圆,AC为直径,点E为 »AC 的中点,点B和点C为线段AD的三等分点。平面AEC外一点F满足FB=...