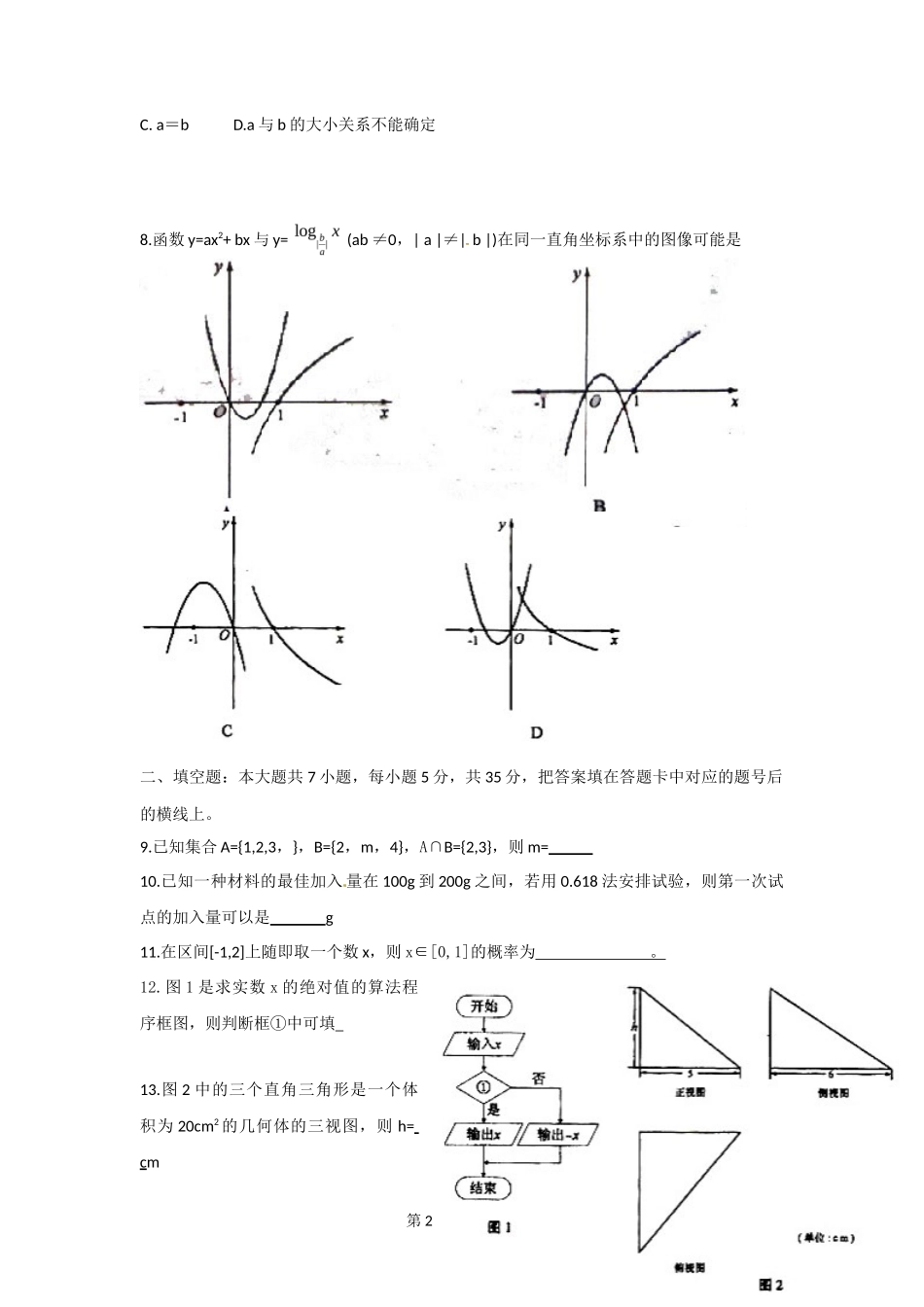
绝密★启封并使用完毕前榆林教学网 http://ylhxjx.com2010 年普通高等学校招生全国统一考试(湖南卷)数学(文史类)一、选择题:本小题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一项符合题目要求的.1. 复数等于A. 1+I B. 1-i C. -1+i D. -1-i2. 下列命题中的假命题是A. B. C. D. 3. 某商品销售量 y(件)与销售价格 x(元/件)负相关,则其回归方程可能是A. B. C. D. 4. 极坐标和参数方程(t 为参数)所表示的图形分别是A. 直线、直线 B. 直线、圆 C. 圆、圆 D. 圆、直线5. 设抛物线上一点 P 到 y 轴的距离是 4,则点 P 到该抛物线焦点的距离是A. 4 B. 6 C. 8 D. 126. 若非零向量 a,b 满足|,则 a 与 b 的夹角为[来源:Zxxk.Com]A. 300 B. 600 C. 1200 D. 15007.在△ABC 中,角 A,B,C 所对的边长分别为 a,b,c,若∠C=120°,c=a,则A.a>b B.a<b第 1 页 | 共 18 页 C. a=b D.a 与 b 的大小关系不能确定榆林教学资源网 http://www.ylhxjx.com8.函数 y=ax2+ bx 与 y= (ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是二、填空题:本大题共 7 小题,每小题 5 分,共 35 分,把答案填在答题卡中对应的题号后的横线上。9.已知集合 A={1,2,3,},B={2,m,4},A∩B={2,3},则 m= 10.已知一种材料的最佳加入 量在 100g 到 200g 之间,若用 0.618 法安排试验,则第一次试点的加入量可以是 g11.在区间[-1,2]上随即取一个数 x,则 x∈[0,1]的概率为 。12.图 1 是求实数 x 的绝对值的算法程序框图,则判断框①中可填 13.图 2 中的三个直角三角形是一个体积为 20cm2 的几何体的三视图,则 h= cm第 2 页 | 共 18 页 14.若不同两点 P,Q 的坐标分别为(a,b),(3-b,3-a),则线段 PQ 的垂直平分线 l 的斜率为 ,圆(x-2)2+(y-3)2=1 关于直线对称的圆的方程为 。 [ 来源 :Z+xx+k.Com] 15. 若 规 定 E=的 子 集为 E 的 第 k 个 子 集 , 其 中 k= ,则(1)是 E 的第____个子集;(2)E 的第 211 个子集是_______三、解答题:本大题共 6 小题,共 75 分,解答应写出文字说明、说明过程或演算步骤。16. (本小题满分 12 分)已知函数(I)求函数的最小正周期。(II) 求函数的最大值及取最大值时 x 的集合。17. (本小题满分 12 分)为了对某课题进行研究,用分层抽样方法从三所高校 A,B,C 的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)(I)求 x,y ;(II)若从高校 B、C 抽取的人中选 2 人作专题发言,求这二人都来自高校 C 的概率。第 3 页 | 共 18 页 18.(本小题满分 12 分)如图所示,在长方体中,AB=AD=1,AA1=2,M 是棱 CC1的中点(Ⅰ)求异面直线 A1M 和 C1D1所成的角的正切值;(Ⅱ)证明:平面 ABM⊥平面 A1B1M119.(本小题满分 13 分)为了考察冰川的融化状况,一支科考队在某冰川山上相距 8Km 的 A、B 两点各建一个考察基地,视冰川面为平面形,以过 A、B 两点的直线为 x 轴 ,线段 AB 的垂直平分线为 y 轴建立平面直角坐标系(图 4)。考察范围到 A、B 两点的距离之和不超过 10Km 的区域。(I)求考察区域边界曲线的方程:(II)如图 4 所示,设线段 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动 0.2km,以后每年移动的距离为前一年的 2 倍。问:经过多长时间,点 A 恰好在冰川边界线上?第 4 页 | 共 18 页 20.(本小题满分 13 分)[来源:学科网]给出下面的数表序列:其中表 n(n=1,2,3 )有 n 行,第 1 行的 n 个数是 1,3,5,2n-1,从第 2 行起,每行中的每个数都等于它肩上的两数之和。(I)写出表 4,验证表 4 各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表 n(n≥3)(不要求证明); (II)每个数列中最后一行都只有一个数,它们构成数列 1,4,12,...