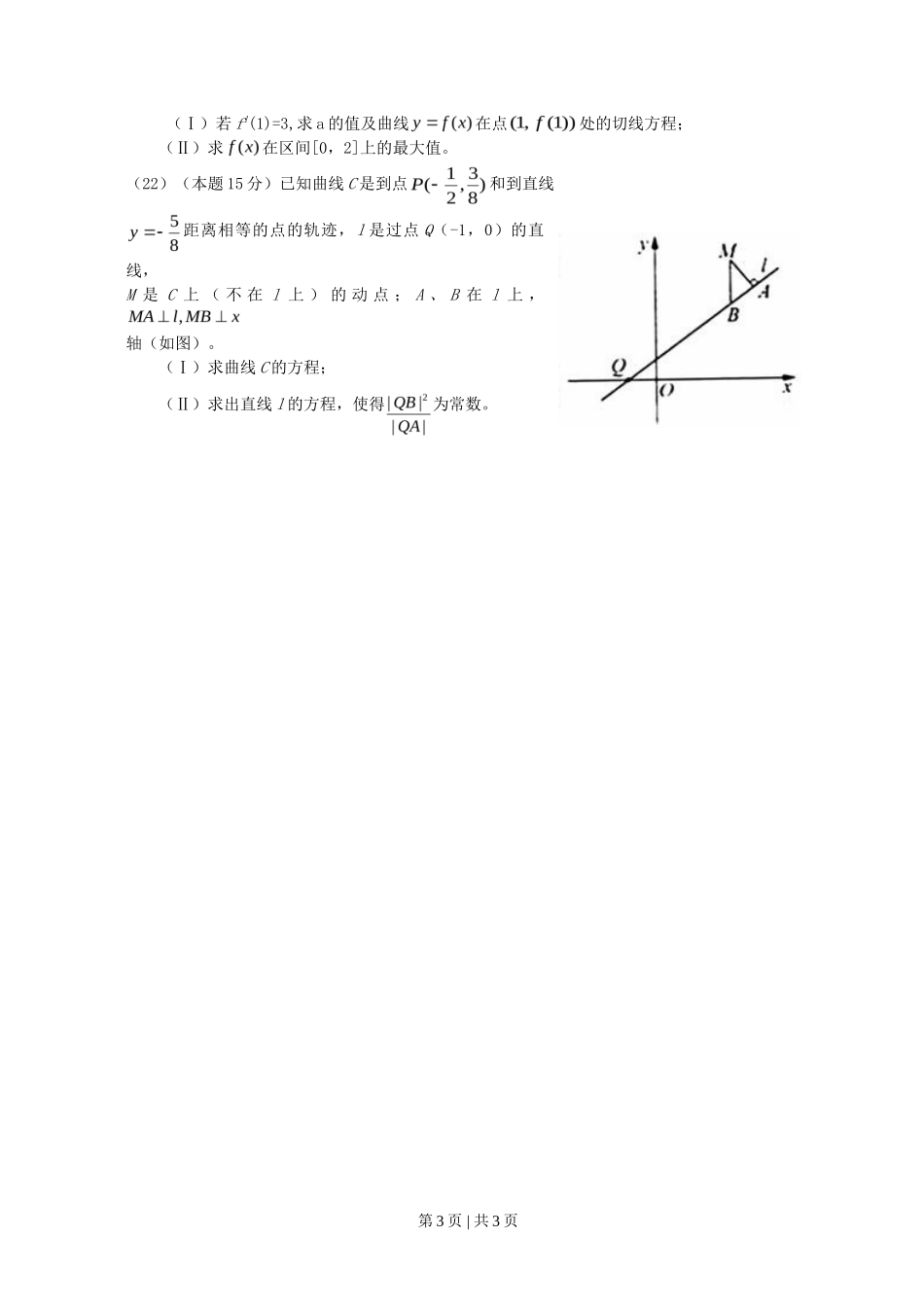
2008 年普通高等学校统一考试(浙江卷)数学(文科)试题第Ⅰ卷 (共 50 分)一、选择题:本大题共 10 小题,每小题 5 分,共 50 分。在每小题给出的四个选项中,只有一项是符合题目要求的。(1)已知集合则=(A)(B) (C) (D) (2)函数的最小正周期是(A)(B)(C) (D) (3)已知 a,b 都是实数,那么“”是“a>b”的(A)充分而不必要条件(B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件(4)已知{an}是等比数列,,则公比 q=(A)(B)-2(C)2(D)(5)已知(A)(B) (C)(D) (6)在(x-1)(x-2)(x-3)(x-4)(x-5)的展开式中,含的项的系数是(A)-15(B)85(C)-120(D)274(7)在同一平面直角坐标系中,函数的图象和直线的交点个数是(A)0(B)1(C)2(D)4(8)若双曲线的两个焦点到一条准线的距离之比为 3:2,则双曲线的离心率是(A)3(B)5(C)(D)(9)对两条不相交的空间直线 a 与 b,必存在平面 α,使得(A)(B)∥α(C)(D)(10)若且当时,恒有,则以 a,b 为坐标的点 P(a,b)所形成的平面区域的面积是第 1 页 | 共 3 页 (A)(B)(C)1(D)第Ⅱ卷(共 100 分)二、填空题:本大题共 7 小题,每小题 4 分,共 28 分。(11)已知函数 .(12)若 .(13)已知 F1、F2为椭圆的两个焦点,过 F1的直线交椭圆于 A、B 两点若|F2A|+|F2B|=12,则|AB|= 。(14)在△ABC 中,角 A、B、C 所对的边分别为 a、b、c。若则 cos A= .(15)如图,已知球 O 的面上四点,DA⊥平面 ABC。AB⊥BC,DA=AB=BC=,则球 O 的体积等于 。(16)已知 a 是平面内的单位向量,若向量 b 满足 b·(a-b)=0,则|b|的取值范围是 .(17)用 1,2,3,4,5,6 组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且 1 和 2 相邻。这样的六位数的个数是 (用数字作答)三、解答题:本大题共 5 小题,共 72 分。解答应写出文字说明、证明过程和演算步骤。(18)(本题 14 分) 已知数列的首项,通项,且成等差数列。求:(Ⅰ)p,q 的值;(Ⅱ) 数列前 n 项和的公式。(19)(本题 14 分)一个袋中装有大小相同的黑球、白球和红球,已知袋中共有 10 个球,从中任意摸出 1 个球,得到黑球的概率是;从中任意摸出 2 个球,至少得到 1 个白球的概率是.求:(Ⅰ)从中任意摸出 2 个球,得到的数是黑球的概率;(Ⅱ)袋中白球的个数。(20)(本题 14 分)如图,矩形 ABCD 和梯形 BEFC 所在平面互相垂直,∠BCF=∠CEF=90°,AD=(Ⅰ)求证:AE∥平面 DCF;(Ⅱ)当 AB 的长为何值时,二面角 A-EF-C 的大小为 60°?( 21 ) ( 本 题 15 分 ) 已 知 a 是 实 数 , 函 数.第 2 页 | 共 3 页 (Ⅰ)若 f1(1)=3,求 a 的值及曲线在点处的切线方程;(Ⅱ)求在区间[0,2]上的最大值。(22)(本题 15 分)已知曲线 C 是到点和到直线距离相等的点的轨迹,l 是过点 Q(-1,0)的直线,M 是 C 上 ( 不 在 l 上 ) 的 动 点 ; A 、 B 在 l 上 ,轴(如图)。(Ⅰ)求曲线 C 的方程;(Ⅱ)求出直线 l 的方程,使得为常数。第 3 页 | 共 3 页