2010年高考数学试卷（理）（湖南）（解析卷）

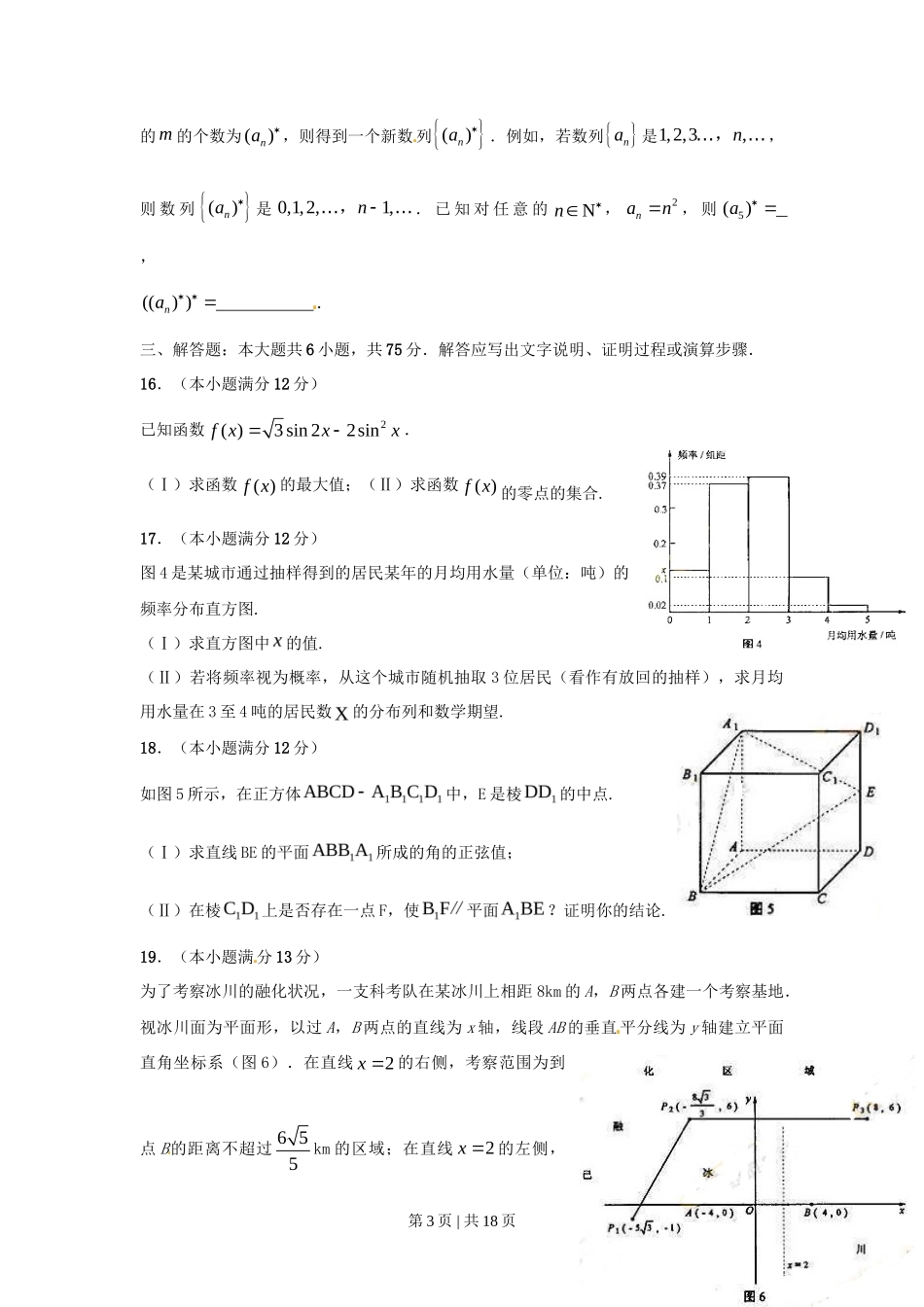
2010 年普通高等学校招生全国统一考试（湖南卷）数学（理工农医类）一、选择题：本大题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只有一项是符合题目要求的．[来源:Z#xx#k.Com]1．已知集合1,2,3M ，2,3,4N ，则A． MN B． NM C．2,3MN  D．1,4MN 2．下列命题中的假命题是A．Rx ，120x ＞ B．Nx ，10x 2＞[来源:Z&xx&k.Com]C．Rx ，lg x＜1 D．Rx ， tan2x 3．极坐标方程cos和参数方程1,23xtyt  （t 为参数）所表示的图形分别是A．圆、直线 B．直线、圆[来源:学+科+网]C．圆、圆 D．直线、直线4．在Rt ABC中，90C ，4AC  ，则 AB AC�等于A． 16 B． 8 C．8 D．165．421dxx等于 A． 2ln 2 B．2ln 2 C．ln 2 D．ln 26．在 ABC中，角 A，B，C 所对的边长分别为 a，b，c．若120C ，2ca，则[来源:学_A．a＞b B．a＜b C．a=b D．a 与 b 的大小关系不能确定7．在某种信息传输过程中，用 4 个数字的一个排列（数字允许重复）表示一个信息，不同排列表示不同信息，若所用数字只有 0 和 1，则与信息 0110 至多有两个对应位置上的数字相同的信息个数为A.10 B.11 C.12 D.158．用min,a b 表示 ,a b 两数中的最小值.若函数( )min,f xxxt的图像关于直线第 1 页 | 共 18 页 12x 对称，则t 的值为 A． 2 B．2 C． 1 D．1二、填空题：本大题共 7 小题，每小题 5 分，共 35 分．把答案填在答题卡中对应题号后的横线上．9．已知一种材料的最佳加入量在 110g 到 210g 之间．若用 0.618 法安排实验，则第一次试点的加入量可以是 g．10．如图 1 所示，过O外一点 P 作一条直线与O交于 A,B 两点．已知 PA=2，点 P 到O的切线长 PT=4，则弦 AB 的长为 ．11．在区间上随机取一个数，则的概率为 ．12．图 2 是求2221232…+100 的值的程序框图，则正整数n  ．13．图 3 中的三个直角三角形是一个体积为 203cm 的几何体的三视图，则h  cm ．14．过抛物线22(0)xpy p＞的焦点作斜率为 1 的 直线与该抛物线交于,A B 两点，,A B在 x 轴上的正射影分别为,D C ．若梯形 ABCD 的面积为12 2 ，则 p  ．15．若数列 na满足：对任意的 nN ，只有有限个正整数 m 使得man＜成立，记这样第 2 页 | 共 18 页 的 m 的个数为()na ，则得到一个新数 列()na ．例如，若数列 na是1,2,3,n…， …，则 数 列 ()na 是 0,1,2,1,n …，…． 已 知 对 任 意 的Nn，2nan， 则5()a  ，(() )na   ．三、解答题：本大题共 6 小题，共 75 分．解答应写出文字说明、证明过程或演算步骤．16．（本小题满分 12 分）已知函数2( )3sin 22sinf xxx．（Ⅰ）求函数( )f x 的最大值；（Ⅱ）求函数( )f x 的零点的集合.17．（本小题满分 12 分）图 4 是某城市通过抽样得到的居民某年的月均用水量（单位：吨）的频率分布直方图.[来源:学.科.网]（Ⅰ）求直方图中的值.（Ⅱ）若将频率视为概率，从这个城市随机抽取 3 位居民（看作有放回的抽样），求月均用水量在 3 至 4 吨的居民数的分布列和数学期望.18．（本小题满分 12 分）如图 5 所示，在正方体中，E 是棱的中点.（Ⅰ）求直线 BE 的平面所成的角的正弦值；（Ⅱ）在棱上是否存在一点 F，使平面？证明你的结论.19．（本小题满分 13 分）为了考察冰川的融化状况，一支科考队在某冰川上相距 8km 的 A，B 两点各建一个考察基地．视冰川面为平面形，以过 A，B 两点的直线为 x 轴，线段 AB 的垂直 平分线为 y 轴建立平面直角坐标系（图 6）．在直线2x  的右侧，考察范围为到点 B的距离不超过 6 55km 的区域；在直线2x  的左侧，第 3 页 | 共 18 页 考察范围为到 A，B 两点的距离之和不超过4 5 k...