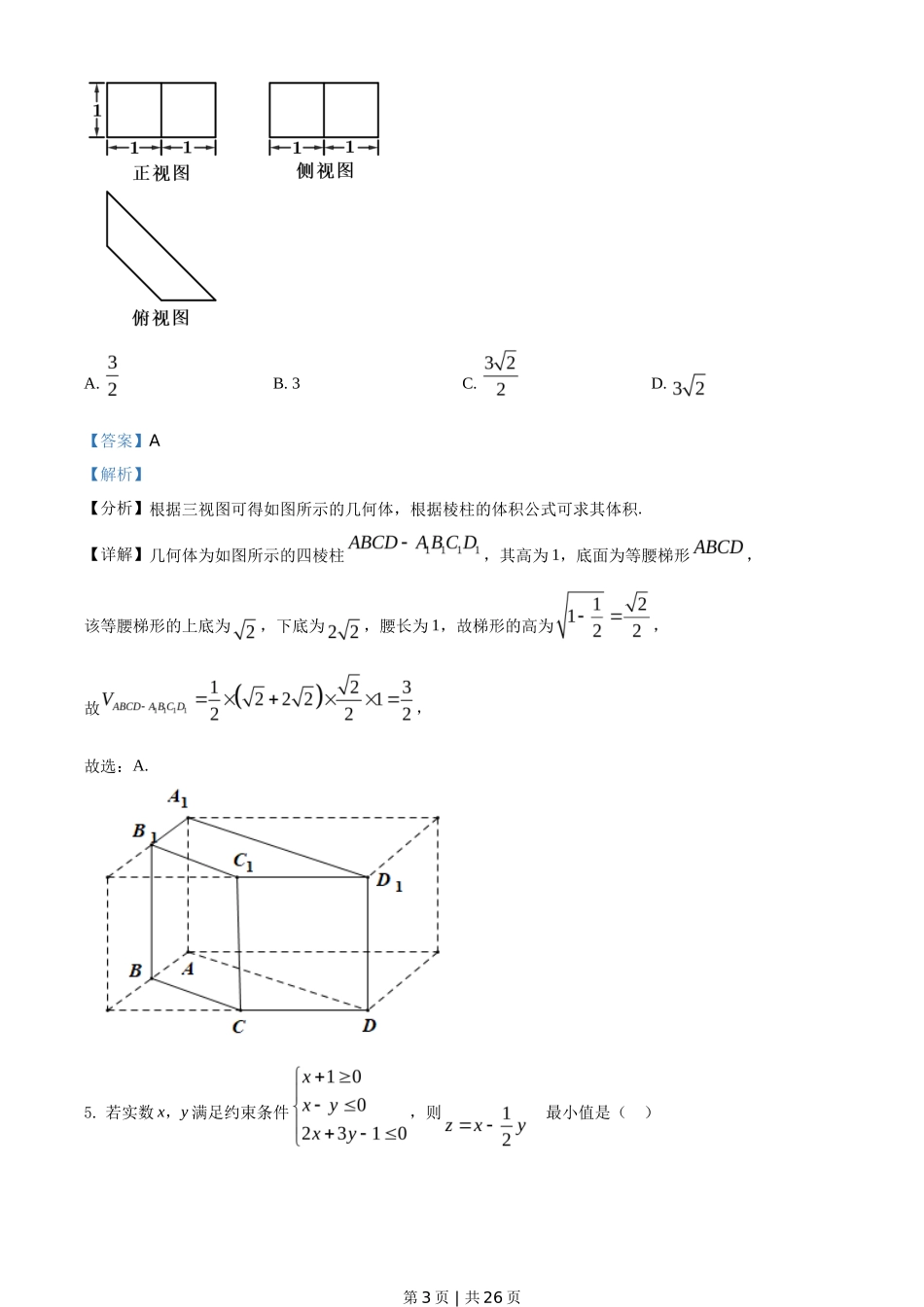
绝密★启用前2021 年普通高等学校招生全国统一考试(浙江卷)数 学本试题卷分选择题和非选择题两部分。全卷共 4 页,选择题部分 1 至 2 页;非选择题部分 3 至 4 页。满分150 分。考试用时 120 分钟。考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。参考公式:如果事件 A,B 互斥,那么()( )( )P ABP AP B 如果事件 A,B 相互独立,那么()( ) ( )P ABP A P B 如果事件 A 在一次试验中发生的概率是 p,那么 n 次独 立 重 复 试 验 中 事 件 A 恰 好 发 生 k 次 的 概 率( )C(1)(0,1,2,, )kkn knnP kppkn台体的体积公式11221 ()3VSS SS h其中12,S S 分别表示台体的上、下底面积,h 表示台体的高柱体的体积公式VSh其中 S 表示柱体的底面积, h 表示柱体的高锥体的体积公式13VSh其中 S 表示锥体的底面积, h 表示锥体的高球的表面积公式24SR 球的体积公式343VR 其中 R 表示球的半径一 选择题、1. 设集合,,则( )A. B. C. D. 【答案】D【解析】【分析】由题意结合交集的定义可得结果.【详解】由交集的定义结合题意可得:.故选:D.2. 已知,,(i 为虚数单位),则( )A. B. 1C. D. 3【答案】C第 1 页 | 共 26 页 【解析】【分析】首先计算左侧的结果,然后结合复数相等的充分必要条件即可求得实数的值.【详解】,利用复数相等的充分必要条件可得:.故选:C.3. 已知非零向量,则“”是“”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件【答案】B【解析】【分析】考虑两者之间的推出关系后可得两者之间的条件关系.【详解】如图所示,,当时,与垂直,,所以成立,此时,∴不是的充分条件,当时,,∴,∴成立,∴是的必要条件,综上,“”是“”的必要不充分条件故选:B.4. 某几何体的三视图如图所示,则该几何体的体积是( )第 2 页 | 共 26 页 A. B. 3C. D. 【答案】A【解析】【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.【详解】几何体为如图所示的四棱柱,其高为 1,底面为等腰梯形,该等腰梯形的上底为,下底为,腰长为 1,故梯形的高为,故,故选:A.5. 若实数 x,y 满足约束条件,则的最小值是( )第 3 页 | 共 26 页 A. B. C. D. 【答案】B【解析】【分析】画出满足条件的可行域,目标函数化为,求出过可行域点,且斜率为的直线在轴上截距的最大值即可.【详解】画出满足约束条件的可行域,如下图所示:目标函数化为,由,解得,设,当直线过点时,取得最小值为.故选:B.6. 如图已知正方体,M,N 分别是,的中点,则( )第 4 页 | 共 26 页 A. 直线与直线垂直,直线平面B. 直线与直线平行,直线平面C. 直线与直线相交,直线平面D. 直线与直线异面,直线平面【答案】A【解析】【分析】由正方体间的垂直、平行关系,可证平面,即可得出结论.【详解】连,在正方体中,M 是的中点,所以为中点,又 N 是的中点,所以,平面平面,所以平面.第 5 页 | 共 26 页 因为不垂直,所以不垂直则不垂直平面,所以选项 B,D 不正确;在正方体中,,平面,所以,,所以平面,平面,所以,且直线是异面直线,所以选项 C 错误,选项 A 正确.故选:A.【点睛】关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.7. 已知函数,则图象为如图的函数可能是( )A. B. C. D. 【答案】D【解析】【分析】由函数的奇偶性可排除 A、B,结合导数判断函数的单调性可判断 C,即可得解.第 6 页 | 共 26 页 【详解】对于 A,,该函数 为非奇非偶函数,与函数图象不符,排除 A;对于 B,,该函数为非奇非偶函数,与...