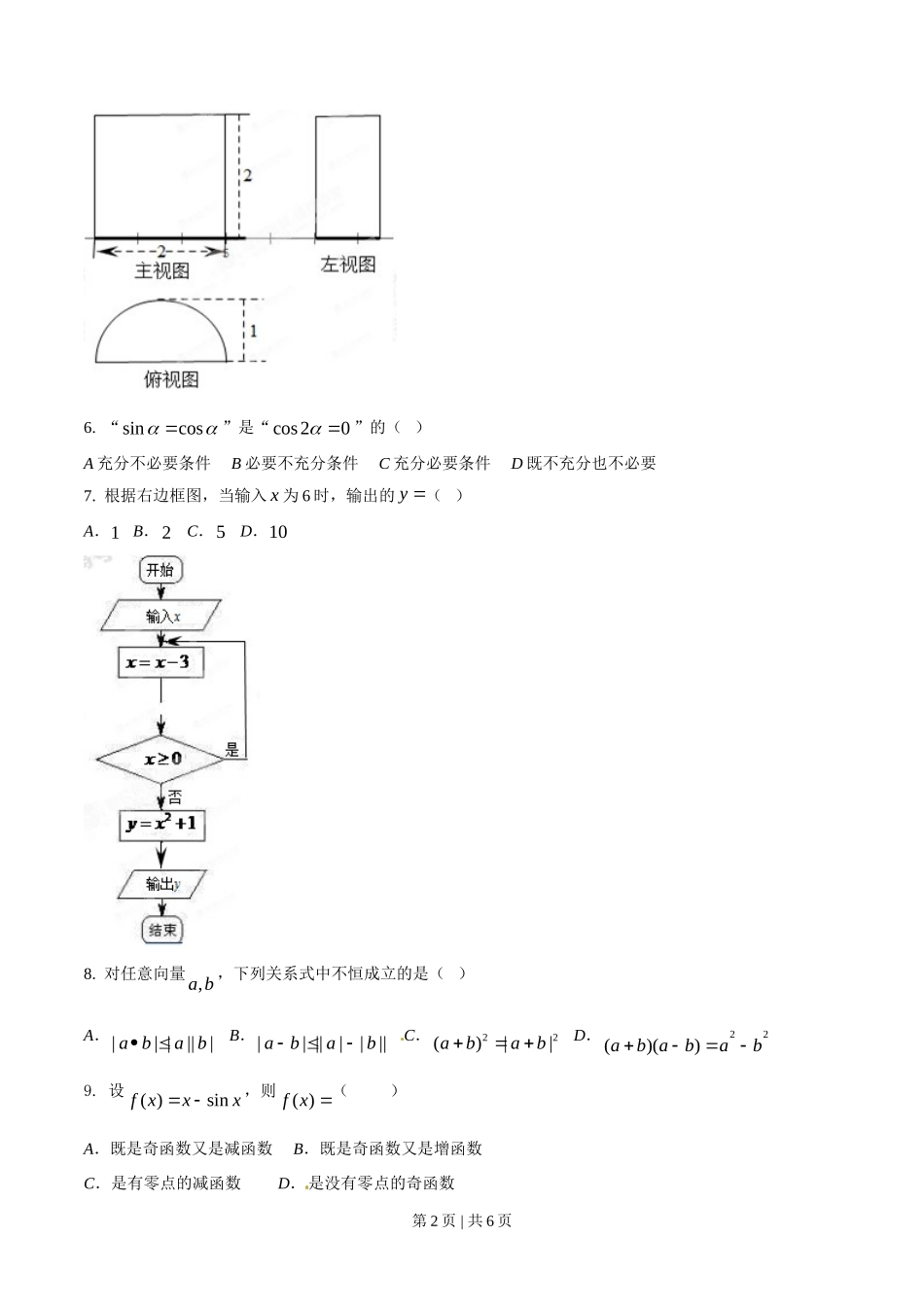
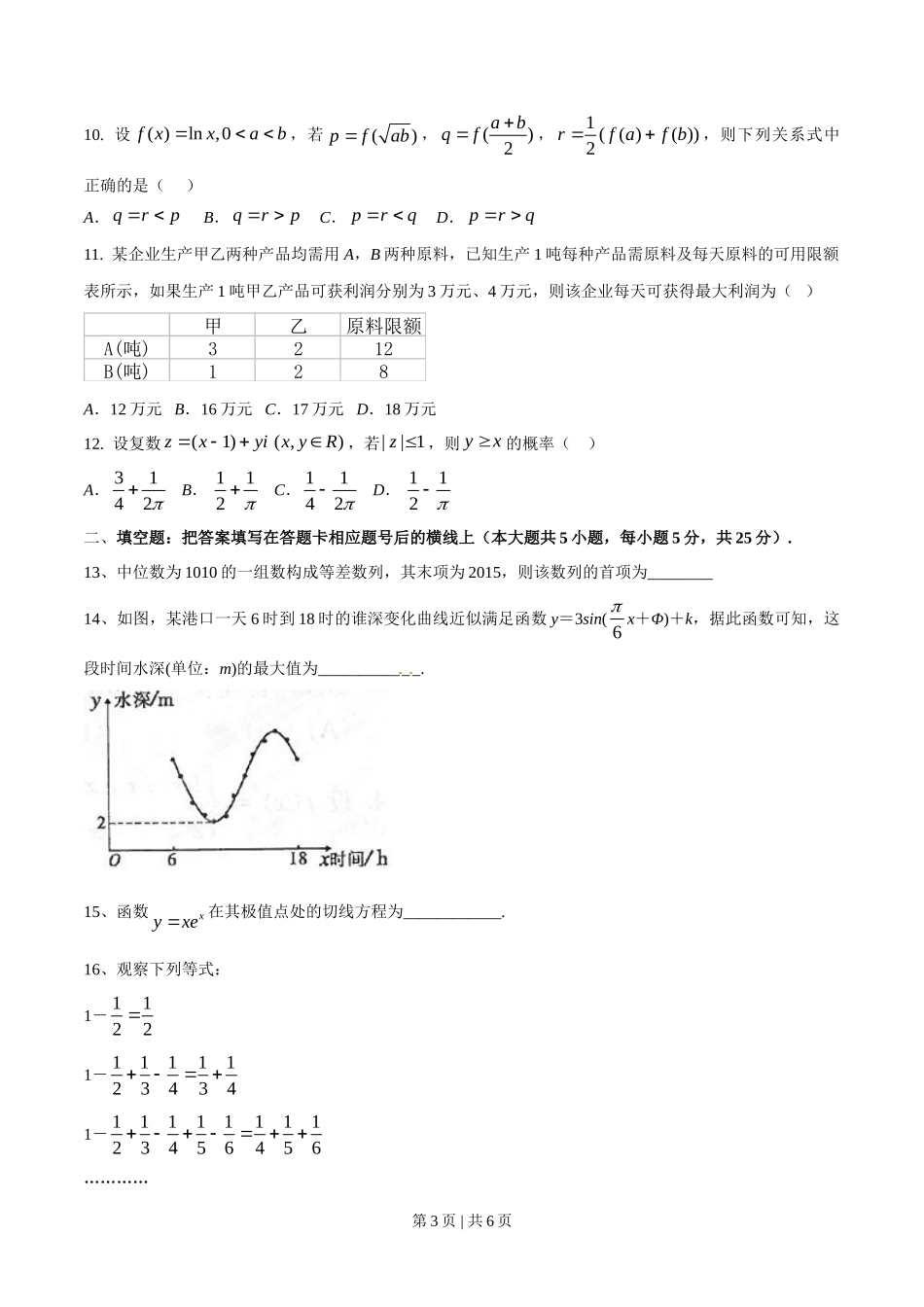
一.选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.(本大题共 10 小题,每小题 5 分,共 50 分).1. 设集合2{ |}Mx xx,{ | lg0}Nxx,则 MN ( )A.[0,1] B.(0,1] C.[0,1) D.(,1] 2. 某中学初中部共有 110 名教师,高中部共有 150 名教师,其性别比例如图所示,则该校女教师的人数为( )A.93 B.123 C.137 D.1673. 已知抛物线22(0)ypx p的准线经过点( 1,1),则抛物线焦点坐标为( )A.( 1,0) B.(1,0) C.(0, 1) D.(0,1)4. 设1,0( )2 ,0xx xf xx ,则( ( 2))f f ( )A. 1 B. 14 C. 12 D. 325. 一个几何体的三视图如图所示,则该几何体的表面积为( )A.3 B.4 C.24 D.34 第 1 页 | 共 6 页 6. “sincos”是“cos20 ”的( )A 充分不必要条件 B 必要不充分条件 C 充分必要条件 D 既不充分也不必要7. 根据右边框图,当输入 x 为 6 时,输出的 y ( )A.1 B.2 C.5 D.108. 对任意向量 ,a b ,下列关系式中不恒成立的是( )A.|| ||||a ba b B.|| ||||||abab C.22()||abab D.22()()ab abab9. 设( )sinf xxx ,则( )f x ( )A.既是奇函数又是减函数 B.既是奇函数又是增函数 C.是有零点的减函数 D.是没有零点的奇函数第 2 页 | 共 6 页 10. 设( )ln ,0f xxab,若()pfab,()2abqf,1 ( ( )( ))2rf af b,则下列关系式中正确的是( )A.qrp B.qrp C. prq D. prq 11. 某企业生产甲乙两种产品均需用 A,B 两种原料,已知生产 1 吨每种产品需原料及每天原料的可用限额表所示,如果生产 1 吨甲乙产品可获利润分别为 3 万元、4 万元,则该企业每天可获得最大利润为( )甲乙原料限额A(吨)3212B(吨)128A.12 万元 B.16 万元 C.17 万元 D.18 万元12. 设复数(1)zxyi( ,)x yR,若|| 1z ,则 yx的概率( )A. 3142 B. 112 C. 1142 D. 112二、填空题:把答案填写在答题卡相应题号后的横线上(本大题共 5 小题,每小题 5 分,共 25 分).13、中位数为 1010 的一组数构成等差数列,其末项为 2015,则该数列的首项为________14、如图,某港口一天 6 时到 18 时的谁深变化曲线近似满足函数 y=3sin( 6 x+Φ)+k,据此函数可知,这段时间水深(单位:m)的最大值为____________.15、函数xyxe在其极值点处的切线方程为____________.16、观察下列等式:1- 11221- 1111123434 1- 1111111123456456 …………第 3 页 | 共 6 页 据此规律,第 n 个等式可为______________________.三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共 6 小题,共 75 分)17. ABC的内角 , ,A B C 所对的边分别为 , ,a b c ,向量( , 3 )mab�与(cos ,sin)nAB平行.(I)求 A ;(II)若7,2ab 求 ABC的面积.18.如图 1,在直角梯形 ABCD 中,//,,2ADBCBADABBC12 ADa , E 是 AD 的中点,O 是OC 与 BE 的交点,将 ABE沿 BE 折起到图 2 中1A BE的位置,得到四棱锥1ABCDE.(I)证明:CD 平面1AOC ;(II)当平面1A BE 平面 BCDE 时,四棱锥1ABCDE的体积为36 2 ,求a 的值.19.随机抽取一个年份,对西安市该年 4 月份的天气情况进行统计,结果如下:日期123456789101112131415天气晴雨阴阴阴雨阴晴晴晴阴晴晴晴晴日期1617181920212223[来源:学科网 ZXXK]24252627282930天气晴阴雨[来源:Z。xx。k.Com]阴阴晴阴晴晴晴阴晴晴晴[来源:学&科&网]雨(I)在 4 月份任取一天,估计西安市在该天不下雨的概率;(II)西安市某学校拟从 4 月份的一个晴天开始举...