专题 解析几何解答题（理科）（学生版）- 十年（-）高考数学真题分项汇编（全国通用）

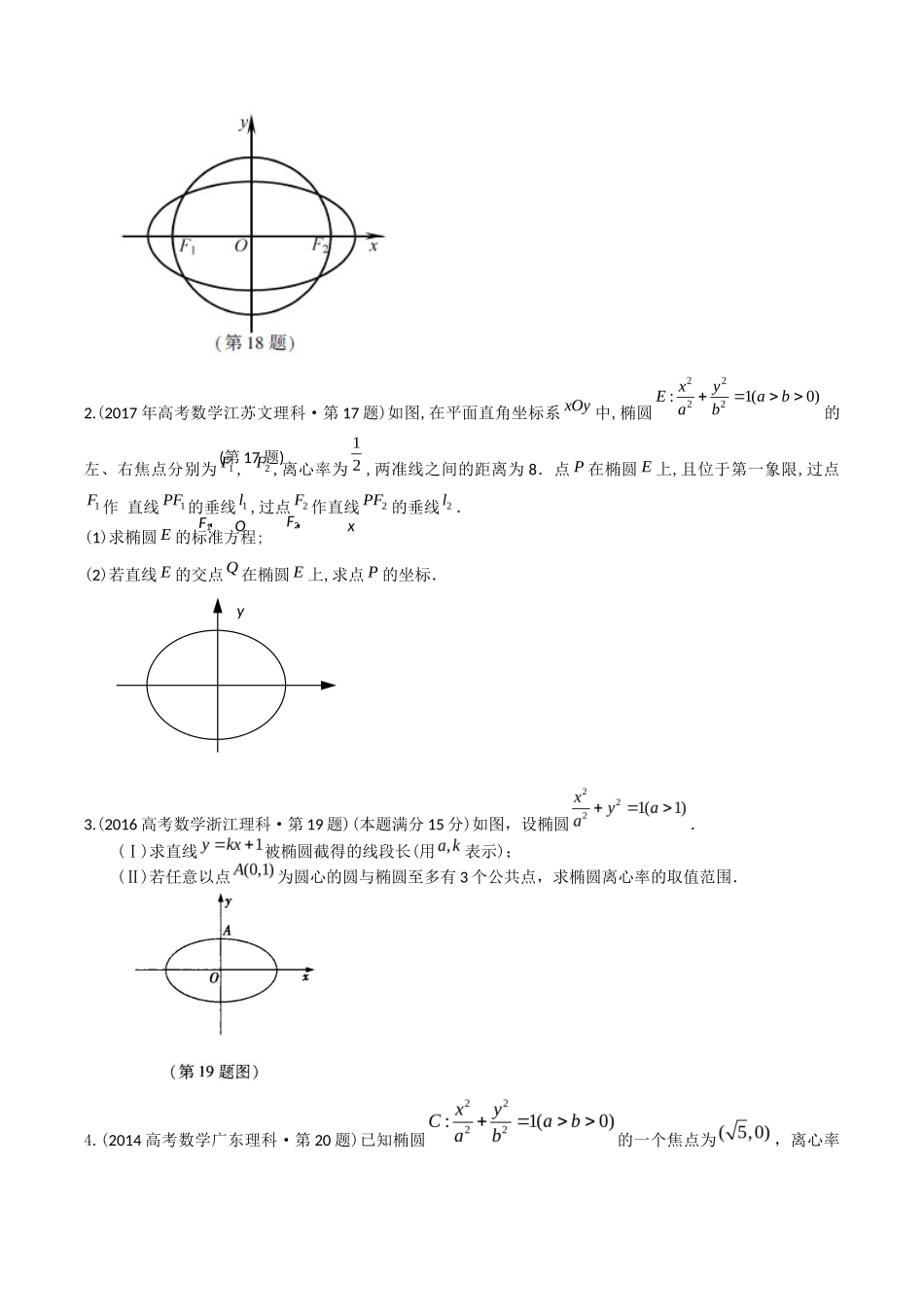
十年（2014－2023）年高考真题分项汇编—解析几何解答题目录题型一：曲线和方程..........................................................................................1题型二：直线与圆的方程.................................................................................3题型三： 椭圆的定义及性质..........................................................................5题型四：直线与椭圆的位置关系....................................................................7题型五：双曲线的定义及性质......................................................................12题型六：直线与双曲线的位置关系.............................................................13题型七：抛物线的定义及性质......................................................................15题型八：直线与抛物线的位置关系.............................................................17题型九：圆锥曲线中的证明问题.................................................................20题型十：圆锥曲线中的最值问题.................................................................22题型十一：圆锥曲线中的综合问题.............................................................25题型一：曲线和方程1.(2018 年高考数学江苏卷·第 18 题)(本小题满分 16 分)如图，在平面直角坐标系中，椭圆 C 过点，焦点，圆 O 的直径为．(1)求椭圆 C 及圆 O 的方程；(2)设直线 l 与圆 O 相切于第一象限内的点 P．①若直线 l 与椭圆 C 有且只有一个公共点，求点 P 的坐标；②直线 l 与椭圆 C 交于两点．若的面积为，求直线 l 的方程．2.(2017 年高考数学江苏文理科·第 17 题)如图,在平面直角坐标系 xOy 中,椭圆2222:1(0)xyEabab的左、右焦点分别为1F , 2F ,离心率为12 ,两准线之间的距离为 8．点 P 在椭圆 E 上,且位于第一象限,过点1F 作 直线1PF 的垂线 1l ,过点2F 作直线2PF 的垂线 2l ．(1)求椭圆 E 的标准方程;(2)若直线 E 的交点Q 在椭圆 E 上,求点 P 的坐标．3.(2016 高考数学浙江理科·第 19 题)(本题满分 15 分)如图，设椭圆．(Ⅰ)求直线被椭圆截得的线段长(用表示)；(Ⅱ)若任意以点为圆心的圆与椭圆至多有 3 个公共点，求椭圆离心率的取值范围．4.(2014 高考数学广东理科·第 20 题)已知椭圆的一个焦点为，离心率(第 17 题)yxF2 O F1为．(1)求椭圆 C 的标准方程；(2)若动点为椭圆 C 外一点，且点 P 到椭圆 C 的两条切线相互垂直，求点的轨迹方程．5.(2017 年高考数学上海(文理科)·第 20 题)(本题满分 16 分,第 1 小题满分 4 分,第 2 小题满分 5 分,第 3 小题满分 7 分)在平面直角坐标系 xOy y 中,已知椭圆22:14xy, A 为  的上顶点, P 为  上异于上、下顶点的动点, M 为 x 正半轴上的动点．(1)若 P 在第一象限,且||2OP ,求 P 的坐标;(2)设8 3( , )5 5P,若以 A 、 P 、 M 为顶点的三角形是直角三角形,求 M 的横坐标;(3)若|| ||MAMP,直线 AQ 与 交于另一点C ,且2AQAC�,4PQPM�,求直线 AQ 的方程． 题型二：直线与圆的方程1．(2015 高考数学福建理科·第 18 题)已知椭圆 E：过点，且离心率为．xyBAOG(Ⅰ)求椭圆 E 的方程；(Ⅱ)设直线交椭圆 E 于 A，B 两点，判断点 G与以线段 AB 为直径的圆的位置关系，并说明理由．2.(2014 高考数学江苏·第 18 题)如图，为了保护河上古桥OA ，规划建一座新桥 BC，同时设立一个圆形保护区．规划要求:新桥 BC 与河岸 AB 垂直;保护区的边界为圆心 M 在线段 OA 上并与 BC 相切的圆．且古桥两端 O 和 A 到该圆上任意一点的距离均不少于 80m． 经测量，点 A 位于点 O 正北方向 60m 处， 点C 位于点 O 正东方向 170m 处(为河岸)，tan∠BCO=43 ．(1)求新桥的长；(2)当多长时，圆形保护区的面积...